- 机率密度函数

机率密度函数
定义
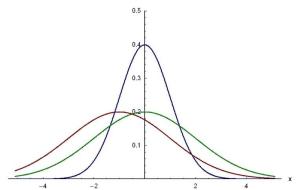 正态分布的概率密度函数对于一维实随机变量X,设它的累积分布函数是
正态分布的概率密度函数对于一维实随机变量X,设它的累积分布函数是![]() ,如果存在可测函数
,如果存在可测函数![]() 满足:
满足: ,那么X是一个连续型随机变量,并且
,那么X是一个连续型随机变量,并且![]() 是它的概率密度函数。
是它的概率密度函数。
连续型随机变量的概率密度函数有如下性质:
如果概率密度函数fX(x)在一点x上连续,那么累积分布函数可导,并且它的导数:
由于随机变量X的取值 只取决于概率密度函数的积分,所以概率密度函数在个别点上的取值并不会影响随机变量的表现。更准确来说,如果一个函数和X的概率密度函数取值不同的点只有有限个、可数无限个或者相对于整个实数轴来说测度为0(是一个零测集),那么这个函数也可以是X的概率密度函数。
连续型的随机变量取值在任意一点的概率都是0。作为推论,连续型随机变量在区间上取值的概率与这个区间是开区间还是闭区间无关。要注意的是,概率P{x=a}=0,但{X=a}并不是不可能事件。[1]
性质
这里指的是一维连续随机变量,多维连续变量也类似。
随机数据的概率密度函数:表示瞬时幅值落在某指定范围内的概率,因此是幅值的函数。它随所取范围的幅值而变化。
密度函数f(x) 具有下列性质:
①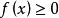 ;
;
②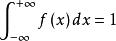 ;
;
③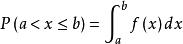
例子
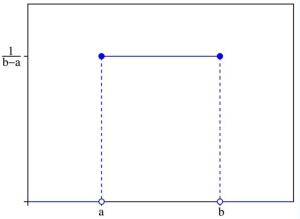 连续型均匀分布的概率密度函数最简单的概率密度函数是均匀分布的密度函数。对于一个取值在区间[a,b]上的均匀分布函数
连续型均匀分布的概率密度函数最简单的概率密度函数是均匀分布的密度函数。对于一个取值在区间[a,b]上的均匀分布函数![]() ,它的概率密度函数:
,它的概率密度函数: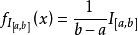
也就是说,当x不在区间[a,b]上的时候,函数值等于0;而在区间[a,b]上的时候,函数值等于这个函数![]() 。这个函数并不是完全的连续函数,但是是可积函数。
。这个函数并不是完全的连续函数,但是是可积函数。
正态分布是重要的概率分布。它的概率密度函数是:
![]()
随着参数μ和σ变化,概率分布也产生变化。
特征函数
对概率密度函数作傅里叶变换可得特征函数。
![]()
特征函数与概率密度函数有一对一的关系。因此知道一个分布的特征函数就等同于知道一个分布的概率密度函数。
应用
随机变量X的n阶矩是X的n次方的数学期望,即
![]()
X的方差为
![]()
更广泛的说,设g为一个有界连续函数,那么随机变量g(X)的数学期望为[1]:
![]()

-
全自动SF6密度继电器校验仪
2025-09-28 06:31:52 查看详情 -
1641函数信号发生器
2025-09-28 06:31:52 查看详情


 求购
求购









