- 二次同余式

二次同余式
基本介绍
二次同余式是关于未知数的二次多项式的同余方程。设正整数![]() ,且
,且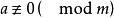 ,则称形如
,则称形如
![]() 的同余式为二次同余式的一般形式,简称模m的二次同余式。此外,称形如
的同余式为二次同余式的一般形式,简称模m的二次同余式。此外,称形如
![]() 的同余式为最简二次同余式,或称最简二次同余方程。满足同余式(1)或(2)的
的同余式为最简二次同余式,或称最简二次同余方程。满足同余式(1)或(2)的![]() 值,分别称为二次同余式(1)或(2)的解,亦称二次同余式的根。若
值,分别称为二次同余式(1)或(2)的解,亦称二次同余式的根。若![]() 为其一解,则
为其一解,则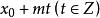 均为其解,即是说若
均为其解,即是说若![]() 适合同余式(1)或(2),则
适合同余式(1)或(2),则![]() 所代表的剩余类中的每一个数皆能适合(1)式或(2)式,但常指该类中的最小正整数为其解,故方程(1)或(2)的解的个数,系指不同剩余类中的能适合(1)式或(2)式的解之个数。二次同余式不一定都有解,如果有解时,其解的个数参见下文“二次同余式的解数”[1]。
所代表的剩余类中的每一个数皆能适合(1)式或(2)式,但常指该类中的最小正整数为其解,故方程(1)或(2)的解的个数,系指不同剩余类中的能适合(1)式或(2)式的解之个数。二次同余式不一定都有解,如果有解时,其解的个数参见下文“二次同余式的解数”[1]。
注意:用![]() 乘式(1)再加上
乘式(1)再加上![]() ,得
,得
![]() 即
即
![]() 若令
若令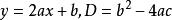 ,则上式变为
,则上式变为
![]() 由同余式的性质可知式(1)与式(3)同时有解或同时无解:故讨论式(1)有解的问题可以转为讨论式(3)有解的问题[2]。
由同余式的性质可知式(1)与式(3)同时有解或同时无解:故讨论式(1)有解的问题可以转为讨论式(3)有解的问题[2]。
二次同余式的解数
二次同余式的解数(solution numbers of a quadratic congruence)是对二次同余式的一种刻画,即二次同余方程解的个数的判定:设![]() 为素数,
为素数,![]() ,且
,且![]() ,二次同余式
,二次同余式
![]()
在![]() 时,解的个数为
时,解的个数为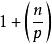 。
。
在![]() 时,解的个数有下面三种情形:
时,解的个数有下面三种情形:
1.![]() ,有一个解;
,有一个解;
2.![]() ,当
,当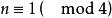 时有二解,
时有二解,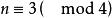 时无解;
时无解;
3.![]() ,当
,当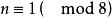 时有四解,
时有四解,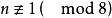 时无解[1]。
时无解[1]。
二次剩余与二次非剩余
为了讨论式(3)是否有解,引入了二次剩余和二次非剩余的概念[2]。
定义设m是正整数,若同余式
![]() 有解,则
有解,则![]() 称为模m的二次剩余(或二次剩余);否则,
称为模m的二次剩余(或二次剩余);否则,![]() 称为模m的二次非剩余(或二次非剩余)。
称为模m的二次非剩余(或二次非剩余)。
下面我们先来讨论模为奇素数p的二次同余式
![]()
定理1(欧拉判别条件)设p是奇素数,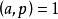 ,则
,则
(1)![]() 是模p的二次剩余的充分必要条件是
是模p的二次剩余的充分必要条件是
![]()
(2)![]() 是模p的二次非剩余的充分必要条件是
是模p的二次非剩余的充分必要条件是
![]() 并且当
并且当![]() 是模p的二次剩余时,式(5)恰有二解。
是模p的二次剩余时,式(5)恰有二解。
推论设p是奇素数,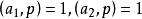 ,则
,则
(1) 如果![]() 都是模p的二次剩余,则
都是模p的二次剩余,则![]() 是模p的二次剩余;
是模p的二次剩余;
(2) 如果![]() 都是模p的二次非剩余,则
都是模p的二次非剩余,则![]() 是模p的二次剩余;
是模p的二次剩余;
(3) 如果![]() 是模p的二次剩余,而
是模p的二次剩余,而![]() 是模p的二次非剩余,则
是模p的二次非剩余,则![]() 是模p的二次非剩余。
是模p的二次非剩余。
定理2设p是奇素数,则模p的简化剩余系中二次剩余与二次非剩余的个数各为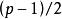 ,且
,且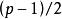 个二次剩余与序列
个二次剩余与序列
![]() 中的一个数同余,且仅与一个数同余[2]。
中的一个数同余,且仅与一个数同余[2]。

-
奥迪二次空气泵电磁阀在哪(奥迪二次空气泵继电器的作用)
2025-09-22 15:31:52 查看详情 -
第二次世界大战在亚洲及太平洋的起源
2025-09-22 15:31:52 查看详情 -
平面二次包络环面蜗杆传动
2025-09-22 15:31:52 查看详情 -
宝骏630图片 宝骏730二次保养多少钱
2025-09-22 15:31:52 查看详情 -
进口普拉多2700 普拉多2700二次空气泵如何清洗
2025-09-22 15:31:52 查看详情 -
宝马黑名单 宝马x1第二次保养需要换什么
2025-09-22 15:31:52 查看详情


 求购
求购





