- Banach代数

Banach代数
定义
代数
定义1 设![]() 是一个线性空间,称
是一个线性空间,称![]() 是一个代数,若:对
是一个代数,若:对![]() 中任意两个元素
中任意两个元素![]() ,规定乘积
,规定乘积![]() ,满足对
,满足对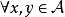 和任意数a,有
和任意数a,有
(1)结合律 x(yz)=(xy)z;
(2)分配律 x(y+z)=xy+xz,(x+y)z=xz+yz;
(3)a(xy)=(ax)y=x(ay).
注:1)设![]() 是一个代数,如果存在
是一个代数,如果存在![]() ,使得
,使得
![]() 就称
就称![]() 是代数
是代数![]() 的一个单位元。
的一个单位元。
2)设![]() 是一个代数,如果
是一个代数,如果![]() ,且
,且![]() 按
按![]() 的线性运算及乘法仍是一个代数,则称
的线性运算及乘法仍是一个代数,则称![]() 是
是![]() 的一个子代数。
的一个子代数。
3)设![]() 是一个代数,当
是一个代数,当![]() 有单位元时,单位元必是唯一的。
有单位元时,单位元必是唯一的。
4)设![]() 是一个有单位元的代数,
是一个有单位元的代数,![]() 且存在
且存在![]() 使得
使得
![]() 其中e为
其中e为![]() 的单位元,则称b为a的逆。[1]
的单位元,则称b为a的逆。[1]
赋范代数
定义2 设![]() 是一个赋范线性空间,同时又是一个代数,而且
是一个赋范线性空间,同时又是一个代数,而且
![]() 则称
则称![]() 是一个赋范代数。[1]
是一个赋范代数。[1]
注:在赋范代数中,关于乘积范数的性质保证了乘法运算的连续性。实际上,当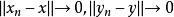 时,
时,
![]()
Banach代数
定义3完备的赋范代数称为Banach代数。[1]
举例
例1 设X是赋范线性空间,则![]() (由X到X的有界线性算子全体)是一个有单位元的赋范代数,X上的恒等算子I 即为其单位元。当X为Banach空间时,
(由X到X的有界线性算子全体)是一个有单位元的赋范代数,X上的恒等算子I 即为其单位元。当X为Banach空间时,![]() 是Banach代数。[1]
是Banach代数。[1]
例2 设X是Banach空间,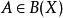 ,
,
![]() 即
即![]() 是与A可交换的有界线性算子全体,显然,
是与A可交换的有界线性算子全体,显然,![]() 是B(X)的一个子代数,而且是闭的,因而也是一个Banach代数。[1]
是B(X)的一个子代数,而且是闭的,因而也是一个Banach代数。[1]
例3 设![]() 是紧拓扑空间,
是紧拓扑空间,![]() 表示
表示![]() 上连续函数全体,对
上连续函数全体,对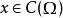 ,令
,令
![]() 则
则![]() 是一个Banach代数。[1]
是一个Banach代数。[1]
谱与谱半径
对于有限维线性空间上的线性变换,特征值是一个十分重要的概念。这个概念拓广到一般的Banach代数中,就是元素的谱。(这里讨论的Banach代数是指复Banach代数。)
定义4 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,
,![]() 为复数,如果存在
为复数,如果存在![]() ,使得
,使得
![]() 即
即![]() 可逆,则称
可逆,则称![]() 为x的正则点,称x的正则点全体为正则集,记作
为x的正则点,称x的正则点全体为正则集,记作![]() ;称非正则点为x的谱点,称x的谱点全体为x的谱集,记作
;称非正则点为x的谱点,称x的谱点全体为x的谱集,记作![]()
定义5 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,记
,记
![]() 称
称![]() 为x的谱半径。[1]
为x的谱半径。[1]
Banach代数的重要性质
定理1 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,则
的Banach代数,则![]() 中可逆元全体是开集,且映射
中可逆元全体是开集,且映射
![]() 在可逆元集合上连续。
在可逆元集合上连续。
定理2 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,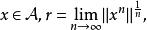 则
则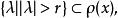 当
当![]() 时,
时,
![]() 且当
且当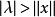 时,
时,
![]()
定理3 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,则
,则![]() 是开集。对
是开集。对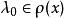 ,记
,记
![]() 则当
则当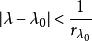 时
时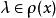 ,且
,且
![]()
定理4 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,则
,则![]() 是闭集,且
是闭集,且
![]()
定理5 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,则谱半径
,则谱半径
![]()
定理6 设![]() 是具有单位元
是具有单位元![]() 的Banach代数,
的Banach代数,![]() ,则
,则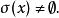
定理7 设![]() 是Banach代数
是Banach代数![]() 的闭子代数,
的闭子代数,![]() 、
、![]() 有相同的单位元,
有相同的单位元,![]() ,则
,则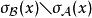 为开集。
为开集。
注:定理1-7的证明见参考文献[1]的59-64页。[1]

-
江铃福特轻客持续打造最优TCO 锐骐超值版PK江铃国产共轨
2025-10-31 04:42:22 查看详情 -
江铃福特轻客持续打造最优TCO 江铃E200N豪华型怎么样
2025-10-31 04:42:22 查看详情 -
380TSI劲擎智联版四驱车型上市 成都车展:雪铁龙C
2025-10-31 04:42:22 查看详情 -
西安大众速腾现金优惠2.3万 成都沃尔沃XC90优惠三万元
2025-10-31 04:42:22 查看详情 -
欧拉新款R1将于成都车展上市 全新宝马2系Coupe最新谍照
2025-10-31 04:42:22 查看详情 -
将于上海车展上市 Ocean曝光
2025-10-31 04:42:22 查看详情 -
保时捷Taycan国内上市 55周年纪念版上市
2025-10-31 04:42:22 查看详情 -
哈尔滨沃尔沃XC40优惠达4.7万 优惠7万元
2025-10-31 04:42:22 查看详情 -
Face家族设计/或年内上市 各限量500台
2025-10-31 04:42:22 查看详情 -
凯迪拉克CT6新车型上市 W帅气亮相
2025-10-31 04:42:22 查看详情


 求购
求购

