朗伯W函数

朗伯 函数的积分形式为

若 ,若

把被积函数的实部和虚部分离出来：

设 ，则有 ，展开分离出实部和虚部，

,当时，易知

若 ，上式还可化为

由隐函数的求导法则，朗伯函数满足以下的微分方程：

，

因此：

，

函数，以及许多含有的表达式，都可以用的变量代换来积分，也就是说

其中为欧米加常数。

、，

其中是高德纳箭号表示法。

、若，则

在的泰勒级数如下：

收敛半径为 。

实部

,

虚部

,

模长

模角

,

共轭值

,

（欧米加常数）

许多含有指数的方程都可以用函数来解出。一般的方法是把未知数都移到方程的一侧，并设法化为的形式，示例如下：

例子1

更一般地，以下的方程

其中

两边同乘: ，

得到：

同除以：，

得到：

同除：，

可以用变量代换

令

化为

即：

同乘：

得出

故

带入

为

因此最终的解为

若辅助方程：中，

,

辅助方程无实数解，原方程亦无实解；

若：,

辅助方程有一实数解，原方程有一实解：

若: ,

辅助方程有二实解，设为，

，

为

例子2

用类似的方法，可知以下方程的解

为

或

例子3

以下方程的解

具有形式

例子4

 :  :

取对数，

取倒数，

最终解为 :

例子5

两边开次方并除以得

令 ，

化为

两边同乘

，

最终得

标准的 Lambert W 函数可用来表示以下超越代数方程式的解：

其中 a0, c   与 r  为实常数。

其解为

Lambert W 函数之一般化 包括:

一项在低维空间内广义相对论与量子力学的应用（量子引力），实际上一种以前未知的 连结 于此二区域中，如 “Journal of Classical and Quantum Gravity” 所示其 (1) 的右边式现为二维多项式 x：

其中 r1 和 r2 是不同实常数，为二维多项式的根。于此函数解有单一引数 x 但 ri  和 ao 为函数的参数。如此一来，此一般式类似于 “hypergeometric”（超几何分布）函数与 “Meijer G“，但属于不同类函数。当 r1 = r2，(2)的两方可分解为 (1) 因此其解简化为标准 W 函数。(2)式代表着 “dilaton”（轴子）场的方程，可据此推导线性，双体重力问题 1+1 维（一空间维与一时间维）当两不等（静止）质量，以及，量子力学的特征能Delta位势阱给不等电位于一维空间。

量子力学的一特例特征能的分析解三体问题，亦即（三维）氢分子离子。于此 (1)（或 (2)）的右手边现为无限级数多项式之比于 x：

其中 ri 与 si 是相异实常数而 x 是特征能和内核距离R之函数。式 (3) 与其特例表示于 (1) 和 (2) 是与一更大类型延迟微分方程。由于哈代的“虚假导数”概念，多根的特殊情况得以解决。

Lambert "W" 函数于基础物理问题之应用并未完全即使标准情况如 (1) 最近在原子，分子，与光学物理领域可见。

朗伯W函数在复平面上的图像

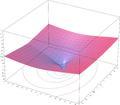
z = Re(W0(x + i y))

z = Im(W0(x + i y))

W函数可以用以下的递推关系算出：