九点圆

1765年，莱昂哈德·欧拉证明：“垂心三角形和垂足三角形有共同的外接圆（六点圆）。”许多人误以为九点圆是由而欧拉发现所以又称乎此圆为欧拉圆。而第一个证明九点圆的人是彭赛列（1821年）。1822年，卡尔·威廉·费尔巴哈也发现了九点圆，并得出“九点圆和三角形的内切圆和旁切圆相切”，因此德国人称此圆为费尔巴哈圆，并称这四个切点为费尔巴哈点。库利奇与大上分别于1910年与1916年发表库利奇－大上定理“圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆。”这个圆还被称为四边形的九点圆，此结果还可推广到n边形。

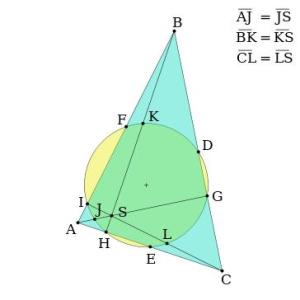
如图：、、为三边的中点，、、为垂足，、、为和顶点到垂心的三条线段的中点。

容易得出、（SAS相似）

因此

同样可得出、（SAS相似）

因此

又，可得出四边形是矩形（四点共圆）

同理可证也是矩形（共圆）

，因此可知也在圆上（圆周角相等）

同理可证、两点也在圆上（九点共圆）

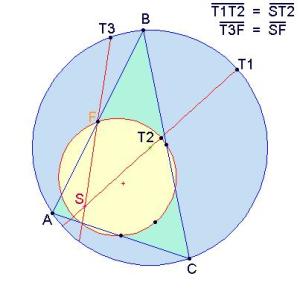
九点圆的半径是外接圆的一半，且九点圆平分垂心与外接圆上的任一点的连线。

在直角坐标系中，我们知道圆的方程为，其中为圆的半径，为圆的圆心坐标。若做圆上三点与点的中点的轨迹，则此轨迹的方程式为：

设为外接圆的半径、为外接圆的圆心坐标、点为垂心坐标。

已知九点圆通过顶点到垂心的三条线段的中点，故此轨迹圆就是九点圆，半径是外接圆的一半，且平分垂心与外接圆上的任一点的连线。

同时还可以得出下面的性质：

圆心在欧拉线上，且在垂心到外心的线段的中点。由此可知，给定三角形顶点座标，九点圆圆心为

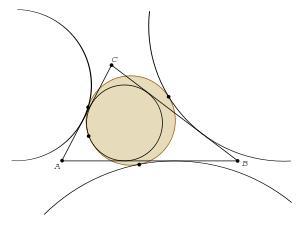
九点圆和三角形的内切圆和旁切圆相切（费尔巴哈定理）。

圆周上四点任取三点做三角形，四个三角形的九点圆圆心共圆（库利奇－大上定理）。

垂心四面体的12点共球 九点圆是垂心四面体各棱的中点和垂足（相对于对棱）共球的特例，两者是同构的

旁心三角形的九点圆是三角形的外接圆

中点三角形的外接圆是三角形的九点圆

三线坐标中，九点圆的座标为

三线坐标中，费尔巴哈点的座标为