1. 向量的模
  1. 首页
  3. 百科
  5. 发动机系统
  7. 向量的模
向量的模

向量的模

中文名 模
别名 向量长度
应用学科 数学
目录导航

含义

向量的大小，也就是向量的长度（或称模），记作。

计算公式

空间向量(x,y,z)，其中x,y,z分别是三轴上的坐标，模长是：

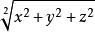
平面向量（x，y），模长是：

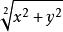
对于向量属于n维复向量空间

=(x1,x2,…,xn)

的模为=

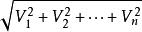
向量的性质

向量的模的运算没有专门的法则，一般都是通过余弦定理计算两个向量的和、差的模。

多个向量的合成用正交分解法，如果要求模一般需要先算出合成后的向量。

模是绝对值在二维和三维空间的推广，可以认为就是向量的长度。推广到高维空间中称为范数。

运算法则

1、模只有大小，是个实数，≥[1]0；

2、=·；

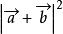3、=+2·+=·+2·+·；

4、≤≤+；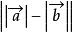

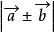5、若=(x，y)，则=

词条图册

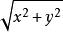
词条图册词条图册(3)

相关百科
返回顶部
产品求购 求购