- 平行向量

平行向量
基本内容
 平行向量(3)向量:既有大小又有方向的量叫向量。
平行向量(3)向量:既有大小又有方向的量叫向量。
零向量:长度为0的向量,记作![]() 。
。
单位向量:长度为1个单位长度的向量。
平行向量:也叫共线向量,方向相同或相反的非零向量。
相等向量:长度相等且方向相同的向量。
相反向量:长度相等且方向相反的向量[1]。
线性运算
加法运算
对于零向量和任意向量![]() ,有:
,有: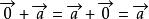 。向量的加法满足所有的加法运算定律。
。向量的加法满足所有的加法运算定律。
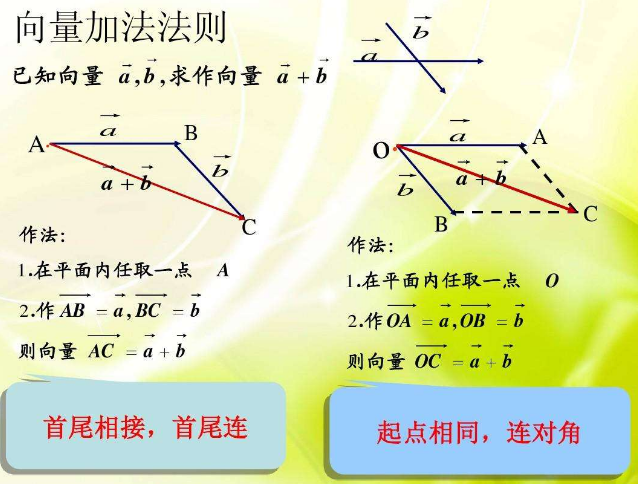
三角形法则:已知从点A出发的向量![]() 与从点B出发的向量
与从点B出发的向量![]() 相加,则以A为起点的向量
相加,则以A为起点的向量![]() 即为它们之和。
即为它们之和。
平行四边形法则:已知两个从同一点O出发的两个向量![]() 、
、![]() ,以OA、OB为邻边作平行四边形OACB,则以O为起点的对角线向量
,以OA、OB为邻边作平行四边形OACB,则以O为起点的对角线向量![]() 就是向量
就是向量![]() 、
、![]() 的和,这种计算法则叫做向量加法的平行四边形法则。
的和,这种计算法则叫做向量加法的平行四边形法则。
减法运算
与![]() 长度相等,方向相反的向量,叫做
长度相等,方向相反的向量,叫做![]() 的相反向量,
的相反向量, ,零向量的相反向量仍然是零向量。
,零向量的相反向量仍然是零向量。
(1)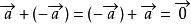 ;(2)
;(2)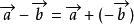 。
。
以减向量的终点为起点,被减向量的终点为终点(三角形法则)[2]。
数乘运算
实数λ与向量![]() 的积是一个向量,这种运算叫做向量的数乘,记作
的积是一个向量,这种运算叫做向量的数乘,记作![]() ,
,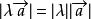 。当λ > 0时,
。当λ > 0时,![]() 的方向和
的方向和![]() 的方向相同,当λ < 0时,
的方向相同,当λ < 0时,![]() 的方向和
的方向和![]() 的方向相反,当λ = 0时,
的方向相反,当λ = 0时,![]() = 0,方向任意。
= 0,方向任意。
设λ、μ是实数,那么:(1)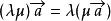 ;(2)
;(2)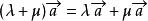 ;
;
(3)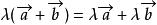 ;(4)
;(4)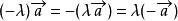 。
。
两个非零向量的数量积: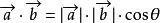 。数量积满足交换律、分配律,不满足结合律[2]。
。数量积满足交换律、分配律,不满足结合律[2]。
充要条件
向量平行(共线)充要条件的两种形式[1]:
(1)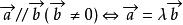 ;
;
(2)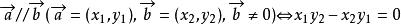 。
。
比较
共线向量与平行向量关系
由于任何一组平行向量都可移到同一直线上,故平行向量也叫做共线向量。
平行向量与相等向量的关系
相等的向量一定平行,但是平行的向量并不一定相等。两个向量相等并不一定这两个向量一定要重合。只用这两个向量长度相等且方向相同即可。其中“方向相同”就包含着向量平行的含义[3]。
例题
例1.下列命题正确的是( )
A.![]() 与
与![]() 共线,
共线,![]() 与
与![]() 共线,则
共线,则![]() 与
与![]() 也共线
也共线
B.任意两个相等的非零向量的始点与终点是一平行四边形的四顶点
C.向量![]() 与
与![]() 不共线,则
不共线,则![]() 与
与![]() 都是非零向量
都是非零向量
D.有相同起点的两个非零向量不平行
解析:由于零向量与任一向量都共线,所以A不正确;由于数学中研究的向量是自由向量,所以两个相等的非零向量可以在同一直线上,而此时就构不成四边形,根本不可能是一个平行四边形的四个顶点,所以B不正确;向量的平行只要方向相同或相反即可,与起点是否相同无关,所以D不正确;对于C,其条件以否定形式给出,所以可从其逆否命题来入手考虑,假若![]() 与
与![]() 不都是非零向量,即
不都是非零向量,即![]() 与
与![]() 至少有一个是零向量,而由零向量与任一向量都共线,可有
至少有一个是零向量,而由零向量与任一向量都共线,可有![]() 与
与![]() 共线,不符合已知条件,所以有
共线,不符合已知条件,所以有![]() 与
与![]() 都是非零向量,所以应选C[3]。
都是非零向量,所以应选C[3]。

-
奔驰S 平行进口实拍
2025-11-01 09:09:16 查看详情 -
天津地区奔驰GLS450 平行进口实拍
2025-11-01 09:09:16 查看详情 -
实拍全新一代奔驰GLE外形怎么样 平行进口实拍
2025-11-01 09:09:16 查看详情 -
静态体验款奔驰E260L 平行进口实拍
2025-11-01 09:09:16 查看详情 -
奔驰R 平行进口实拍
2025-11-01 09:09:16 查看详情


 求购
求购



