双线性函数

若V是有限维的，φ是V上的双线性函数，且α1，α2，…，αn是V的基，则对α，β∈V，有

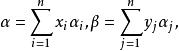及

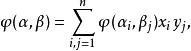即若以α，β表示定义域为V的变量，则域P上n维线性空间V上的双线性函数φ(α，β)可以表示为域P上变量x1，x2，…，xn与y1，y2，…，yn的双线性型。^[1]

1.以φ(αi，αj)作为(i，j)元素的n阶矩阵(φ(αi，αj)ij)称为双线性函数φ关于给定基的矩阵。^[1]

2.V上的双线性函数φ关于不同基的矩阵A，B相互合同：A=XBX，其中X是原基底到新基底的过渡矩阵。^[1]

3.φ关于基的矩阵(aij)的秩亦称为φ的秩。^[1]

4.当(aij)非退化时，φ亦称为非退化的或满秩的。^[1]

5.当(aij)为对称(反对称)矩阵时，φ亦称为对称(反对称)双线性函数。^[1]

半双线性函数（sesquilinear function）是双线性函数的推广。设P为域，J是P的自同构，域中元素k在J下的像记为kJ，而V1，V2是域P上的线性空间，V1×V2到P上的映射φ，若满足：

1.对任意k1，k2∈P，α1，α2∈V1，β∈V2，有

φ(k1α1+k2α2，β)=k1φ(α1，β)+k2φ(α2，β);

2.对任意k1，k2∈P，α∈V1，β1，β2∈V2，有

φ(α，k1β1+k2β2)=k1Jφ(α，β1)+k2Jφ(α，β2);

则称φ为V1×V2上关于J的半双线性函数。^[1]

注：1.当J为恒等自同构时，半双线性函数即双线性函数。

2.V×V上关于J的半双线性函数φ称为V上的半双线性函数。

3.V中向量α，β在V上半双线性函数φ下的像φ(α，β)称为α与β的内积或纯量积，常简记为(α，β)。当(α，β)=0时，称α与β左正交，也称β与α右正交。^[1]