- 圆锥曲线硬解定理

圆锥曲线硬解定理
定理简介
在将圆锥曲线的方程与直线方程联立求解时人们发现了可消项的存在。但其一般化的推导结果不具有普适性,且一直无法用一个简洁的形式表示.。由CGY(2010)以椭圆曲线推导,重新排列分组形式,并引入ε,从而得出了较为简洁的表示形式。后再由CGY成功引入弦长计算公式,并将适用范围扩大到对y值求解与对x的求解,从而奠定了CGY-EH定理强大的通用性与普适性。
定理内容
若曲线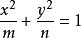 与直线
与直线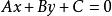 相交于
相交于![]() 两点,则:
两点,则:
![]()
![]()
![]()
![]()
其中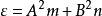 ;
;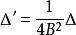 。
。
定理说明
应用该定理于
①椭圆时:
焦点位x轴时: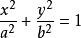 ,应将
,应将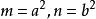 代入。
代入。
焦点位于y轴时: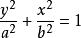 ,应将
,应将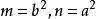 代入。
代入。
②双曲线时:
焦点位于x轴时: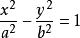 ,应将
,应将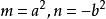 代入,同时
代入,同时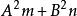 不应为零,即
不应为零,即![]() 不为零;
不为零;
焦点位于y轴时: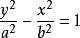 ,应将
,应将 代入,同时
代入,同时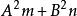 不应为零,即
不应为零,即![]() 不为零
不为零
求解![]() 与
与![]() 时,只须将
时,只须将![]() 与
与![]() 的值互换且
的值互换且![]() 与
与![]() 的值互换。可知
的值互换。可知![]() 与
与![]() 的值不会因此而改变。
的值不会因此而改变。
定理补充
联立曲线方程与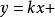
![]() 是现行高考中比联立
是现行高考中比联立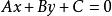 更为普遍的现象。其中联立后的二次方程是标准答案中必不可少的一项,
更为普遍的现象。其中联立后的二次方程是标准答案中必不可少的一项,![]() ,
,![]() 都可以直接通过韦达定理求得,唯独弦长的表达式需要大量计算。这里给出一个CGY-EH的斜率式简化公式,以减少记忆量,以便在考试中套用。
都可以直接通过韦达定理求得,唯独弦长的表达式需要大量计算。这里给出一个CGY-EH的斜率式简化公式,以减少记忆量,以便在考试中套用。
若曲线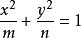 与直线:
与直线: 相交于
相交于![]() 两点,则:
两点,则:
![]()
![]()
这里的![]() 既可以是常数,也可以是关于
既可以是常数,也可以是关于![]() 的代数式。
的代数式。
由这个公式我们可以推出:
若曲线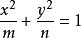 为椭圆:
为椭圆: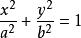
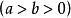 ,则
,则
![]()
若曲线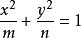 为双曲线:
为双曲线: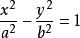 ,则
,则
![]()
由于在高考中CGY-EH定理不可以直接应用,因此现提供参考解题步骤:
解:
由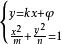 ,得
,得![]()
![]()
设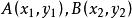
由韦达定理,得: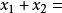
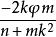 ①,
①,![]()
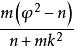 ②;
②;
由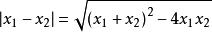 ,代入①②式,化简得:
,代入①②式,化简得: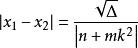
所以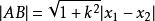
注:对于椭圆: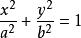
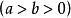 与直线:
与直线: ,联立得:
,联立得:
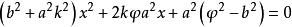 ;
;
对于双曲线: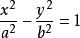
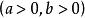 与直线:
与直线: ,联立得:
,联立得:
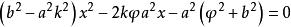
定理简证
设曲线: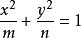 (mn
(mn![]() 0,且m,n不同时为负数)与直线:
0,且m,n不同时为负数)与直线: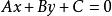
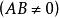 相交于E、F两点,联立两式,得二次方程:
相交于E、F两点,联立两式,得二次方程:
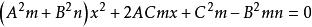
![]()
根据韦达定理,得:
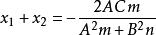
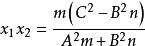
由于![]() 的意义仅在于正负性,且
的意义仅在于正负性,且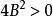 恒成立,可令
恒成立,可令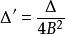 ,则
,则![]() 与
与![]() 同号
同号
由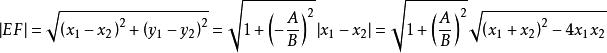
(或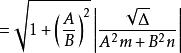 )
)
可得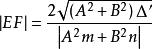
令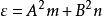 ,则可得CGY-EH定理:
,则可得CGY-EH定理:
![]()
![]()
![]()
![]()

-
杜诗赵次公先后解辑校
2025-11-02 14:42:12 查看详情 -
为什么奥迪q5刹车硬(奥迪q5刹车硬什么原因)
2025-11-02 14:42:12 查看详情 -
2011版全国大学生电子设计竞赛试题精解
2025-11-02 14:42:12 查看详情


 求购
求购









