- 二次不等式

二次不等式
定义
当不等式两端是含有n个(n是自然数)未知数的整式时,则根据整式的次数分别叫做n元一次不等式,n元二次不等式等等。例如,不等式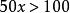 是一元一次不等式,
是一元一次不等式,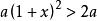 是一元二次不等式;而不等式
是一元二次不等式;而不等式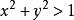 则是二元二次不等式。[1]二次不等式(quadratic inequality)是一种整式不等式,如果整式不等式的次数是2,则称为二次不等式,若二次不等式有n个未知数,则称为n元二次不等式。
则是二元二次不等式。[1]二次不等式(quadratic inequality)是一种整式不等式,如果整式不等式的次数是2,则称为二次不等式,若二次不等式有n个未知数,则称为n元二次不等式。
一元二次不等式
定义:含有一个未知数,且的未知数的最高次数是二次的不等式叫作一元二次不等式。
一元二次不等式的解法:
(1)一元二次不等式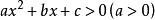 ,设相应的一元二次方程
,设相应的一元二次方程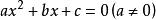 的两根为
的两根为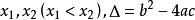 。
。
若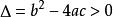 ,一元二次不等式的解集为
,一元二次不等式的解集为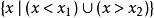 ;
;
若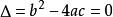 ,一元二次不等式的解集为
,一元二次不等式的解集为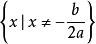 ;
;
若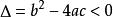 ,解集为R。
,解集为R。
(2)一元二次不等式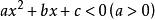 ,设相应的一元二次方程
,设相应的一元二次方程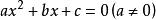 的两根为
的两根为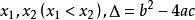 。
。
若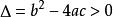 ,一元二次不等式的解集为
,一元二次不等式的解集为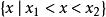 ;
;
若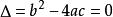 ,一元二次不等式的解集为
,一元二次不等式的解集为![]() ;
;
若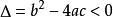 ,一元二次不等式的解集为
,一元二次不等式的解集为![]() 。[2]
。[2]
二元二次不等式
定义1一个二元二次方程表示一条圆锥曲线,为简便计,这里只研究具有标准形式(非退化)的圆锥曲线方程所对应的不等式表示的区域。
定义2平面![]() 上所有满足二元二次不等式
上所有满足二元二次不等式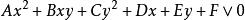 (
(![]() 不全为零)的点的集合,叫作这个二元二次不等式表示的区域,这里“V”表示“>”,“<”,“≥”,“≤”四种中的一种。
不全为零)的点的集合,叫作这个二元二次不等式表示的区域,这里“V”表示“>”,“<”,“≥”,“≤”四种中的一种。
定理1在曲线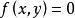 所划分的每个平面开区域
所划分的每个平面开区域![]() 内,多项式
内,多项式![]() 或者永远是正的,或者永远是负的。
或者永远是正的,或者永远是负的。
定理2不等式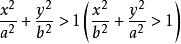 表示椭圆
表示椭圆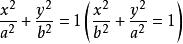 的外部的开区域;不等式
的外部的开区域;不等式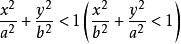 表示椭圆的内部的开区域(图1,图2)。
表示椭圆的内部的开区域(图1,图2)。
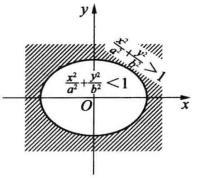 图1
图1
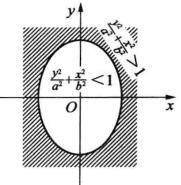 图2
图2
定义3设圆锥曲线方程c:
![]() 称含有焦点的区域为圆锥曲线的内域,不含焦点的区域为圆锥曲线的外域(证明过程请参考相应参考资料)。
称含有焦点的区域为圆锥曲线的内域,不含焦点的区域为圆锥曲线的外域(证明过程请参考相应参考资料)。
定理3点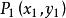 和
和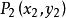 在(1)的同一区域(或不同区域)的充要条件是[3]
在(1)的同一区域(或不同区域)的充要条件是[3]
![]()
定理4点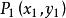 在圆锥曲线
在圆锥曲线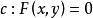 的内域(或外域)的充要条件是
的内域(或外域)的充要条件是
![]() 其中
其中
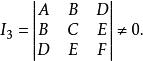
推论: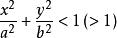 的解域是椭圆
的解域是椭圆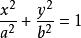 的内域(或外域);
的内域(或外域);
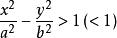 的解域是双曲线
的解域是双曲线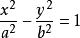 的内域(或外域);
的内域(或外域);
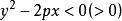 的解域是抛物线
的解域是抛物线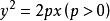 的内域(或外域)。
的内域(或外域)。

-
奥迪二次空气泵电磁阀在哪(奥迪二次空气泵继电器的作用)
2025-09-26 22:15:15 查看详情 -
第二次世界大战在亚洲及太平洋的起源
2025-09-26 22:15:15 查看详情 -
平面二次包络环面蜗杆传动
2025-09-26 22:15:15 查看详情 -
宝骏630图片 宝骏730二次保养多少钱
2025-09-26 22:15:15 查看详情 -
进口普拉多2700 普拉多2700二次空气泵如何清洗
2025-09-26 22:15:15 查看详情 -
宝马黑名单 宝马x1第二次保养需要换什么
2025-09-26 22:15:15 查看详情


 求购
求购





