- 点到直线距离

点到直线距离
公式整理
一、总公式:
设直线 L 的方程为Ax+By+C=0,点 P 的坐标为(x0,y0),则点 P 到直线 L 的距离为:
考虑点(x0,y0,z0)与空间直线x-x1/l=y-y1/m=z-z1/n,有d=|(x1-x0,y1-y0,z1-z0)×(l,m,n)|/√(l²+m²+n²)
二、引申公式:
公式①:设直线l1的方程为;直线l2的方程为
则 2条平行线之间的间距:
公式②:设直线l1的方程为;直线l2的方程为
则 2条直线的夹角
知识与技能目标
(1)理解点到直线距离公式的推导过程,并且会使用公式求出定点到定直线的距离;
(2)了解两条平行直线的距离公式,并能推导的平方
过程与方法目标:
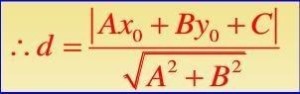 (1)通过对点到直线距离公式的推导,提高学生对数形结合的认识,加深用“计算”来处理“图形”的意识;
(1)通过对点到直线距离公式的推导,提高学生对数形结合的认识,加深用“计算”来处理“图形”的意识;
(2)把两条平行直线的距离关系转化为点到直线距离。
证明方法
- 定义法证:根据定义,点P(x₀,y₀)到直线l:Ax+By+C=0的距离是点P到直线l的垂线段的长,设点P到直线的垂线为l',垂足为Q,则l'的斜率为B/A则l'的解析式为y-y₀=(B/A)(x-x₀)把l和l'联立得l与l'的交点Q的坐标为((B^2x₀-ABy₀-AC)/(A^2+B^2), (A^2y₀-ABx₀-BC)/(A^2+B^2))由两点间距离公式得
PQ^2=[(B^2x₀-ABy₀-AC)/(A^2+B^2)-x0]^2
+[(A^2y₀-ABx₀-BC)/(A^2+B^2)-y0]^2
=[(-A^2x₀-ABy₀-AC)/(A^2+B^2)]^2
+[(-ABx₀-B^2y₀-BC)/(A^2+B^2)]^2
=[A(-By₀-C-Ax₀)/(A^2+B^2)]^2
+[B(-Ax₀-C-By₀)/(A^2+B^2)]^2
=A^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
+B^2(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(A^2+B^2)(Ax₀+By₀+C)^2/(A^2+B^2)^2
=(Ax₀+By₀+C)^2/(A^2+B^2)
所以PQ=|Ax₀+By₀+C|/√(A^2+B^2),公式得证。
二、函数法
证:点P到直线上任意一点的距离的最小值就是点P到直线的距离。在上取任意点用两点的距离公式有,为了利用条件上式变形一下,配凑系数处理得:
当且仅当时取等号所以最小值就是
三、不等式法
证:点P到直线上任意一点Q的距离的最小值就是点P到直线的距离。由柯西不等式:
当且仅当时取等号所以最小值就是
四、转化法
证:设直线的倾斜角为过点P作PM∥轴交于M显然所以
易得∠MPQ=(图2)或∠MPQ=(图3)
在两种情况下都有所以
五、三角形法
证:P作PM∥轴交于M,过点P作PN∥轴交于N(图4)
由解法三知;同理得
在Rt△MPN中,PQ是斜边上的高
六、参数方程法
证:过点作直线交直线于点Q。(如图1)
由直线参数方程的几何意义知,将代入得
整理后得
当时,我们讨论与的倾斜角的关系:
当为锐角时()有(图2)
当为钝角时()有(图3)
得到的结果和上述形式相同,将此结果代入①得
七、向量法
证:如图五,设直线的一个法向量,Q直线上任意一点,则。从而点P到直线的距离为:
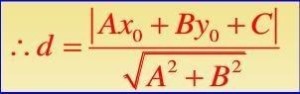

-
直线电机轮轨交通牵引传动系统
2025-09-21 09:10:45 查看详情 -
天津保税区汽车城 天津港保税区汽车城和奥特莱斯距离远吗
2025-09-21 09:10:45 查看详情 -
淄博汽车网 淄博下午到莱芜的长途车,都是几点发车?几点到?
2025-09-21 09:10:45 查看详情 -
直线行驶比转弯省油吗
2025-09-21 09:10:45 查看详情


 求购
求购






