连续小波变换

连续小波变换，通常是用来将连续时间的函数分解成小波。相较于傅立叶变换，连续小波转换不一样的地方在于它能将处理的讯号在建构时频表示时拥有良好的时间和频率的定位。

的连续小波变换为：

其中 为母小波， 中a的为控制尺度，b的部分为控制位置，a和b均为任意实数。

恢复原信号x(t)的第一种逆变换为：

其中：

一般称为小波容许性常数，小波容许性常数需要满足：

上式也被常常称为小波容许性条件。

恢复原信号x(t)的第二种逆变换为：

这种逆变换定义小波为：

其中为窗函数。定义这种小波的目的是为了对信号进行标准时频分析，因此可以称之为分析小波。分析小波不用满足容许性条件。

由定义上来看，连续小波变换式可视为输入的一连串资料和母小波之间的折积。折积的部分可以利用快速傅立叶变换得到；一般来说，除非母小波本身是复数，那么通常连续小波变换输出的Xw(a,b) 会是一个实数值的函数。而一个复数的母小波则会将连续小波变换的结果变成一个复数值的函数。而连续小波变换的功率则可由| Xw(a,b) |绝对值平方得到。

加伯变换在处理讯号时不管是高频或是低频，尺度皆是相同的

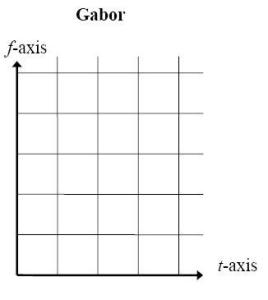CwtcomparetoGabor.jpg

而小波转换则会根据不同的频率改变其本身的的尺度

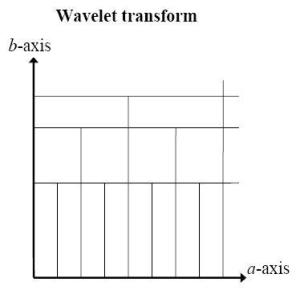CompareCwttogabor.jpg

小波变换的分辨率在a-axis中，不因a值的改变而改变，但延著不同的b值改变以得到较好的结果。