函数的奇偶性

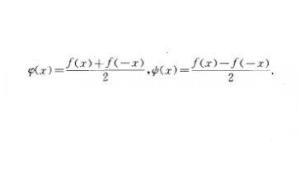函数的奇偶性函数的奇偶性(odevity of a function)，对任意xEl，若f(-x)=f(x)，即在关于y轴的对称点的函数值相等，则f(x)称为偶函数;若f(-x)= - f(x)，即对称点的函数值正负相反，则f(x)称为奇函数.在平面直角坐标系中，偶函数的图象对称于y轴，奇函数的图象对称于原点.可导的奇(偶)函数的导函数的奇偶性与原来函数相反.定义在对称区间(或点集)上的任何函数f(x)都可以表示成奇函数φ( x)和偶函数ψ(x)之和。

函数的奇偶性定义

定理 奇函数图象关于原点成中心对称图形

f(x)为奇函数，f(x)的图象关于原点对称，如图1：

奇函数在某一区间上单调递增，则在它的对称区间上也是单调递增。

点（x,y）→（-x,-y）

奇函数图像关于原点对称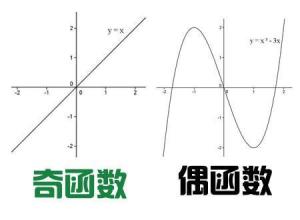图1 函数图像

定理 偶函数的图象关于y轴成轴对称图形

f(x）为偶函数，f(x)的图象关于Y轴对称，如图1

点（x,y）→（-x,y）

偶函数在某一区间上单调递减，则在它的对称区间上单调递增。

偶函数关于Y轴对称

1、利用奇偶函数的定义来判断（这是最基本，最常用的方法）定义：如果对于函数y=f（x）的定义域A内的任意一个值x，都有f（-x）=-f（x）则这个函数叫做奇函数f（-x）=f（x），则这个函数叫做偶函数

2、用求和（差）法判断：

若f（x）-f（-x）=2f（x），则f（x）为奇函数。

若f（x）+f（-x）=2f（x），则f（x）为偶函数。

3、用求商法判断

若=-1,（f（x）≠0）则f（x）为奇函数

若=1,（f（x）≠0）则f（x）为偶函数

1、大部分偶函数没有反函数（因为大部分偶函数在整个定义域内非单调函数）。

2、偶函数在定义域内关于y轴对称的两个区间上单调性相反，奇函数在定义域内关于原点对称的两个区间上单调性相同。

3、奇±奇=奇（可能为既奇又偶函数） 偶±偶=偶（可能为既奇又偶函数） 奇X奇=偶 偶X偶=偶 奇X偶=奇（两函数定义域要关于原点对称）.

4、对于F（x）=f[g(x)]：

若g(x）是偶函数且f（x）是偶函数，则F[x]是偶函数。

若g(x) 是偶函数且f（x）是奇函数，则F[x]是偶函数。

若g(x）是奇函数且f(x）是奇函数，则F[x]是奇函数。

若g(x）是奇函数且f(x）是偶函数，则F[x]是偶函数。

5、奇函数与偶函数的定义域必须关于原点对称。

[1]奇偶性是整体性质；

[2]x在定义域中，那么-x在定义域中吗？----具有奇偶性的函数，其定义域必定是关于原点对称的；

[3]f(-x)=f(x)的等价形式为：f(x)-f(-x)=0，=1（f（x）≠0）

f(-x)=-f(x)的等价形式为：f(x)+f(-x)=0；=-1（f（x）≠0）

[4]由定义不难得出若一个函数是奇函数且在原点有定义，则必有f(0)=0；

[5]既是奇函数，又是偶函数的函数有无数个，只要f（x）=0，且定义域关于原点对称即可