超几何分布

超几何分布(3)产品抽样检查中经常遇到一类实际问题，假定在N件产品中有M件不合格品，即不合格率。

在产品中随机抽n件做检查，发现k件不合格品的概率为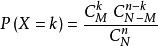,max{0,n+M-N}≦k≦min{n,M}。

亦可写作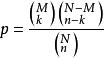（与上式不同的是M可为任意实数，而C表示的组合数M为非负整数）

为古典概型的组合形式，a为下限，b为上限，此时我们称随机变量X服从超几何分布（hypergeometric distribution）。

需要注意的是：^[1]

（1）超几何分布的模型是不放回抽样。

（2）超几何分布中的参数是N,n,M，上述超几何分布记作X~H(N,n,M)。

已经知道某个事件的发生概率，判断从中取出一个小样本，该事件以某一个机率出现的概率问题。

例：在一个口袋中装有30个球，其中有10个红球，其余为白球，这些球除颜色外完全相同。游戏者一次从中摸出5个球。摸到至少4个红球就中一等奖，那么获一等奖的概率是多少？

解：由题意可见此问题归结为超几何分布模型。

其中N = 30. D = 10. n = 5.

P（一等奖） = P(X=4） + P(X=5）

由公式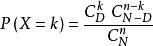,k=0,1,2,...得：

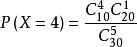
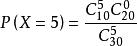
P（一等奖） = 106/3393

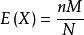对X~H(n,M,N) ,.^[2]

证明：

引理一：∑{C(x,a)*C(d-x,b),x=0..min{a,d}}=C(d,a+b），考察（1+x)^a*（1+x)^b中x^d的系数即得。（另：还可以由超几何分布1=∑P(X=K),k=0,1,2....n得）

引理二：k*C(k,n)=n*C(k-1,n-1），易得。

正式证明：

EX=∑{k*C(k,M)*C(n-k,N-M)/C(n,N),k=0..min{M,n}}

=1/C(n,N)*∑{M*C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}

//（提取公因式，同时用引理二变形，注意k的取值改变）

=M/C(n,N)*∑{C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}} （提取，整理出引理一的前提）

=M*C(n-1,N-1）/C(n,N) （利用引理一）

=Mn/N （化简即得）

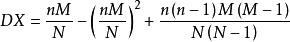对X~H(n,M,N) ,.^[2]

证明：

DX=E(X^2）-(EX)^2 （此公式利用定义式简单展开即得）

=∑{k^2*C(k,M)*C(n-k,N-M)/C(n,N),k=0..min{M,n}}-(Mn/N)^2

=1/C(n,N)*∑{M*k*C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2（提取，变形）

=M/C(n,N)*∑{(k-1）*C(k-1,M-1）*C(n-k,N-M)+C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2

（拆项，变形）

=M/C(n,N)*∑{(M-1）*C(k-2,M-2）*C(n-k,N-M),k=2..min{M,n}}+M/C(n,N)*∑{C(k-1,M-1）*C(n-k,N-M),k=1..min{M,n}}-(Mn/N)^2 （拆开∑，就是分组求和）

=M(M-1）*C(n-2,N-2）/C(n,N)+Mn/N-(Mn/N)^2

=nM(N-M)(N-n)/[(N^2）（N-1）] （化简即得）

超几何分布和二项分布的联系^[1]

（1）在超几何分布中，当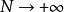时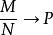，(二项分布中的p）。

（2）当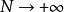时，超几何分布的数学期望

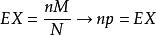
（3）当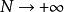时，超几何分布的方差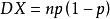（二项分布的方差）。

（4）当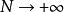时，超几何分布近似为二项分布。

超几何分布计算函数

function HYPGEOMDIST(kkk,n,MM,NN)

for k=kkk to n

AA=1

BBA=1

BBB=1

lll=n

for i= 0 to k-1

BBA=BBA*(MM-i)/(NN-i)

next

for j= k to n

BBB=BBB*(NN-MM-j+k)/(NN-j)

next

BBs=BBB*BBA

if lll-k>k then

x=K

Else x=lll-k

end if

for i=1 to x

lll=lll-1

next

HYPGEOMDIST=HYPGEOMDIST+BBS

next

end function

response.write HYPGEOMDIST（200,2200,1000,17000)

%>