- 复对称矩阵

复对称矩阵
基本介绍
复对称矩阵指aij=aji(i,j=1,2,…,n)的n阶复矩阵A=(aij)。任何n阶复矩阵相似于复对称矩阵,任何复对称矩阵S正交相似于对称矩阵![]() ,即存在正交矩阵T,使
,即存在正交矩阵T,使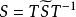 ,其中
,其中
![]() 是准对角形矩阵,子块E(p)是p阶单位矩阵,子块
是准对角形矩阵,子块E(p)是p阶单位矩阵,子块
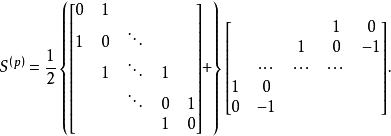
![]() 称为复对称矩阵S的标准形[1]。
称为复对称矩阵S的标准形[1]。
相关分析
矩阵A∈Mn是对称的,是指A=AT,在许多场合,所研究的对称矩阵只有实元素,因而它们是实Hermite矩阵[2]。
但是,在有些情形,我们要与复对称矩阵打交道,一个例子是研究复平面中单位圆盘的正则解析映射,如果f(z)是单位圆盘上的正则解析函数,又如果f(z)是适合f(0)=0和f'(0)=1的标准化了的函数,那么,f(z)是一一的(有时称为单叶的), 当且仅当
 对满足|zi|<1的点
对满足|zi|<1的点 ∈C的所有选择,点
∈C的所有选择,点 ∈C的所有选择和所有n=1,2,...成立。如果
∈C的所有选择和所有n=1,2,...成立。如果![]() ,则右边的差商可以看作f'(zi)。这些称为Grunsky不等式组的庞杂不等式有很简单的代数形式
,则右边的差商可以看作f'(zi)。这些称为Grunsky不等式组的庞杂不等式有很简单的代数形式
![]() 其中
其中 ,
,
![]()
![]()
应注意的是,A是Hermite矩阵,而B是复对称矩阵。
另一个自然要产生复对称矩阵的例子出现在一般的矩问题中。设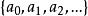 是给定的复数序列,设n≥1是某个正整数,且定义
是给定的复数序列,设n≥1是某个正整数,且定义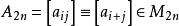 ,注意A2n是形状为Hankel矩阵的复对称矩阵。对x∈C2n,我们考虑复二次型
,注意A2n是形状为Hankel矩阵的复对称矩阵。对x∈C2n,我们考虑复二次型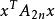 ,要问是否存在某个固定常数c>0,使得对所有x∈C2n和所有n=1,2,...有
,要问是否存在某个固定常数c>0,使得对所有x∈C2n和所有n=1,2,...有
![]() 根据Nebari定理,这个条件成立, 当且仅当存在一个几乎处处有界的Lebesgue可测函数F(t): F(t):R→C,它的Fourier系数是已知数
根据Nebari定理,这个条件成立, 当且仅当存在一个几乎处处有界的Lebesgue可测函数F(t): F(t):R→C,它的Fourier系数是已知数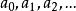 ;关于F(t)的本质边界恰好是上述不等式组的常数c。
;关于F(t)的本质边界恰好是上述不等式组的常数c。
在实际应用中复对称矩阵似乎不像复Hermite(或实对称)矩阵那样几乎经常出现,但是前两个例子说明,它们还是出现了,虽然复对称矩阵不一定可对角化,可是复对称矩阵有一个类似于Hermite 矩阵的谱定理的分解,并且可以用逻辑上类似的方法来证明它,我们首先证明一个与Schur三角分解定理类似的定理,它说明,包括对称矩阵在内的一类矩阵总可以分解成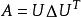 ,其中U是西矩阵,
,其中U是西矩阵,![]() 是上三角矩阵,如果,上三角矩阵是对称的,则它必定是对角矩阵[2]。
是上三角矩阵,如果,上三角矩阵是对称的,则它必定是对角矩阵[2]。
定理1设A∈Mn是给定的,那么存在西矩阵U∈Mn和上三角矩阵![]() ∈Mn使得
∈Mn使得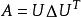 ,当且仅当
,当且仅当![]() 的所有特征值是非负实数,在这个条件下,
的所有特征值是非负实数,在这个条件下,![]() 的所有主对角元可以选取非负值。
的所有主对角元可以选取非负值。
每个对称矩阵A∈Mn有如下性质: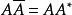 的所有特征值都是非负的。该特殊形式已包含在上述定理中,人们通常把它归功于Schur(1945). 但是较早的证明是由Hua(1944),Siegel(1943)和Jacobsen(1939)提出的;而历史的优先权显然应该属于Takagi(1925)。
的所有特征值都是非负的。该特殊形式已包含在上述定理中,人们通常把它归功于Schur(1945). 但是较早的证明是由Hua(1944),Siegel(1943)和Jacobsen(1939)提出的;而历史的优先权显然应该属于Takagi(1925)。
推论(Takagi分解) 如果A∈Mn是对称矩阵(A=AT),则存在西矩阵U∈Mn和非负实对角矩阵Σ=diag(σ₁,..σn)使得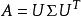 。U的诸列是由
。U的诸列是由![]() 的特征向量组成的标准正交组,而Σ的相应对角元是
的特征向量组成的标准正交组,而Σ的相应对角元是![]() 的相应特征值的非负平方根[2]。
的相应特征值的非负平方根[2]。

-
江铃宝典堪称商用皮卡常青树 江铃新宝典VS长城风骏7(图文)
2025-10-18 02:49:06 查看详情 -
江铃宝典堪称商用皮卡常青树 和江铃域虎9来一场户外探索
2025-10-18 02:49:06 查看详情 -
江铃宝典堪称商用皮卡常青树 抓住秋天的尾巴
2025-10-18 02:49:06 查看详情 -
四肢呈对称性下运动神经元性瘫痪
2025-10-18 02:49:06 查看详情 -
互联网用户账号名称管理规定
2025-10-18 02:49:06 查看详情 -
奥迪如何设置车内蓝牙名称(奥迪怎么设置车内蓝牙名称)
2025-10-18 02:49:06 查看详情 -
河南汽车衡厂家解决称重企业的难点(动态汽车衡是地磅吗)
2025-10-18 02:49:06 查看详情 -
江铃宝典堪称商用皮卡常青树 新增5/7座车型
2025-10-18 02:49:06 查看详情 -
大型多人在线第一人称射击游戏
2025-10-18 02:49:06 查看详情


 求购
求购





