n维欧几里得空间

在解析几何和数学分析中，我们对一维欧几里得空间R¹(即R，实直线)，二维欧几里得空间R²(即实平面)和三维欧几里得空间R³(即现实的三维立体空间)有了比较深入的了解。现在，我们讨论n维欧几里得空间。

定义1设n是正整数，由n个实数构成的有序数组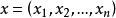的全体组成的集合，称为n维点集或n维欧几里得空间，记作Rⁿ，即^[2]

为了深入研究行维点集Rⁿ中邻域、有界集、点列收敛等概念，需要对Rⁿ中的点之间定义距离。为了使问题讨论适用于更广泛的情形，我们对一般的集合给出距离的概念^[2]。

定义2设X是一个非空集合，如果对于X中任何两个元素x和y，都有一个确定的实数，记为ρ(x，y)，与之对应，且满足下面三个条件，则称ρ是X上的一个距离，称ρ(x，y)是x和y之间的距离，而称X是以ρ为距离的距离空间(或度量空间)，记为(X，ρ)。这三个条件是：

(1)非负性，ρ(x，y)≥0，而且ρ(x，y)=0当且仅当x=y；

(2)对称性，ρ(x，y)=ρ(y，z)；

(3)三角不等式，ρ(x，y)≤ρ(x，z)+ρ(z，y)，这里z也是X中的任意一个元素。

对于Rⁿ中的任意两点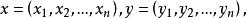定义实函数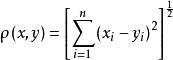，则ρ(x，y)满足距离的三个条件(1)，(2)，(3)，称ρ为Rⁿ上的欧几里得距离，称(Rⁿ，ρ)为n维欧几里得空间。

定义3设P0∈Rⁿ是一固定点，δ>0为一实数，则集合{P|ρ(P，P0)<δ)称为以P0为中心的δ邻域，记作U(P0，δ)。

P0称为邻域的中心，δ称为邻域的半径，某邻域当不需要指出半径时，可以简单地说是P0的某邻域，记作U(P0)，显然，在R，R2，R3中的邻域U(P0，δ)，就分别是以P0为中心以δ为半径的开区间、开圆和开球。

容易证明邻域具有如下基本性质：

(1)对于Q∈U(P)，存在U(Q)U(P)；

(2)对于P≠Q，存在U(P)和U(Q)，使U(P)∩U(Q)=∅。

定义4设{Pk)是Rn中一个点列，P0∈Rn，如果当k→∞时，有ρ(Pk，P0)→0，则称点列{Pk}收敛于P0，记为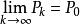或。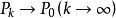

用邻域的语言来说，就是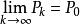：对P0的任意邻域U(P0)，存在K∈N+，使当k>K时，Pk∈U(P0)．

用“ε一N”语言来说，就是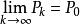：对任意的ε>0，存在K∈N+，使当k>K时，ρ(Pk，P0)<ε．

定义5设A，B是两个非空点集，A与B的距离定义为^[2]