- 可逆线性变换

可逆线性变换
可逆线性变换的定义
设σ是线性空间V的一个线性变换,如果存在V的另一个变换τ,使得
![]() 则称线性变换σ为可逆的,并称τ为σ的逆。
则称线性变换σ为可逆的,并称τ为σ的逆。
显然,当σ可逆时,它的逆是唯一的,将σ的唯一逆记为σ-1。
线性变换σ的逆σ-1也是V的线性变换,称为σ的逆变换。
当σ是可逆线性变换时,还可以定义σ的负整数次幂σ-n=(σ-1)n,其中n是非负整数。
这样,对于可逆线性变换σ来说,
![]() 其中m,n可以是任意整数[2]。
其中m,n可以是任意整数[2]。
相关性质及证明
定理1设σ是线性空间V的一个线性变换,称:
Ker(σ)= {α∈V|σ(α)=0}
为σ的核;称:
Im(σ) =σ(V) = {σ(α)|α∈V}
为σ的像(或值域),Ker(σ)与σ(V)都是V的子空间,且:
dim Ker(σ) + dimσ(V) =n.
证明:容易看出Ker(σ)是V的子空间。现在证明:σ(V)也是V的子空间[2]。
设ξ,η是σ( V)的任意两个向量,那么总存在α,β∈V,使得ξ=σ(α),η=σ(β),因为σ是V的线性变换,于是对于任意a,b∈F,有:
aξ+bη=aσ(α) +bσ(β) =σ(aα+bβ)∈σ(V),
这就证明了σ(V)也是V的一个子空间。
设dim Ker(σ) =r,在Ker(σ)中取一个基{α1;...,αr},它可以扩充为V的一个基{α1;...,αr,αr+1;...,αn},则:
{σ(αr+1),...,σ(αn)}
是像空间σ(V)的一个基。事实上,显然有:
σ(V)=span{σ(α1),.. ,σ(αr),σ(αr+1),.. ,σ(αn)}.
注意到σ(α1)=σ(α2)=...=σ(αr)=0,因此:
σ(V) =span{σ(αr+1),...,σ(αn)}.
若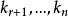 ∈F使得kr+1σ(αr+1)+...+knσ(αn)=0,则:
∈F使得kr+1σ(αr+1)+...+knσ(αn)=0,则:
σ(kr+1αr+1+...+knαn)=0,
于是,kr+1αr+1+...+knαn∈Ker(σ),因此存在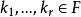 使得:
使得:
kr+1αr+1+...+knαn=k1α1+...+knαn
又α1;...,αr,αr+1;...,αn线性无关,故k1=...=kr=kr+1=...=kn=0,由此可见:σ(αr+1),...,σ(αn)线性无关,因此σ(αr+1),...,σ(αn)组成σ(V)的一个基,并且dimσ(V) =n-r,故dim Ker(σ) + dimσ(V) =n。
怎样来判别一个线性变换是否可逆呢?一般来说,一个变换可逆的充分必要条件是这个变换既是单射又是满射。但是,从定理1出发,可以得到有限维线性空间上的线性变换具有一个很好的性质。
推论1n维线性空间V.上的线性变换σ是单射的充分必要条件是σ是满射。
证明显然,线性变换σ是单射的充分必要条件为Ker(σ)= {0},而:
Ker(σ)={0}![]() dim Ker(σ)=0
dim Ker(σ)=0![]() dimσ(V)=n
dimσ(V)=n![]() σ(V)=V,
σ(V)=V,
因此,线性变换σ是单射的充分必要条件是σ是满射。
对于线性空间V和W之间的线性映射σ,同样可以引进核Ker(σ)与σ(V)像的概念,并且可以证明:Ker(σ)是V的子空间,σ(V)是W的子空间[2]

-
非线性方程组数值解法
2025-09-23 13:29:35 查看详情 -
非线性阈值协整理论及其在中国的应用研究
2025-09-23 13:29:35 查看详情


 求购
求购










