- 指数族分布

指数族分布
中文名
指数族分布
所属学科
数学
别称
指数型分布族
基本介绍
借助指数族分布,对响应变量Y的描述将不再局限于正态分布,称观测 来自指数族分布,如果其概率密度函数可以表达为如下形式:
来自指数族分布,如果其概率密度函数可以表达为如下形式:
![]() 其中:
其中:
(1)![]() 是指数族的自然参数(natural parameter),是我们感兴趣的参数;
是指数族的自然参数(natural parameter),是我们感兴趣的参数;![]() 称为尺度参数或讨厌参数;
称为尺度参数或讨厌参数;
(2)![]() 以及
以及![]() 是依据不同指数族而确定的函数。注意
是依据不同指数族而确定的函数。注意![]() 只由
只由![]() 和
和![]() 决定。
决定。
指数族的均值和方差
指数族的均值、方差都有简洁的表达式。由于
![]() 因此可知随机变量
因此可知随机变量![]() 的均值为
的均值为
![]() 此外,由于
此外,由于
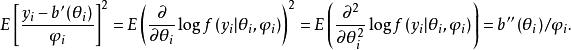 可以得到方差公式
可以得到方差公式
![]()
常见指数族分布
指数族包含了很多常用的概率分布。例如,正态分布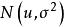 的密度函数为
的密度函数为
![]() 上式可以化为(1)式的形式
上式可以化为(1)式的形式
![]() 对应于(1)式,我们有
对应于(1)式,我们有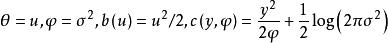 。由此可见,正态分布属于(1)式所定义的概率指数族。
。由此可见,正态分布属于(1)式所定义的概率指数族。
同样的,Bernoulli分布![]() 也属于指数族,这是因为它的概率密度函数
也属于指数族,这是因为它的概率密度函数
![]() 可以化为
可以化为
![]() 再令
再令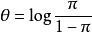 可得
可得
![]() 对应于(1)式,我们有
对应于(1)式,我们有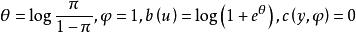 。
。
此外,泊松分布![]() 的密度函数为
的密度函数为
![]() 伽马分布
伽马分布![]() 的密度函数为
的密度函数为
![]() 泊松分布
泊松分布![]() 和伽马分布
和伽马分布![]() 都属于指数族,下表总结了所有的指数族分布[1]。
都属于指数族,下表总结了所有的指数族分布[1]。
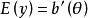 |
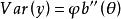 |
||||
正态分布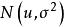 |
|||||
| 两点分布 |
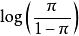 |
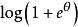 |
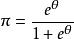 |
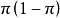 |
|
二项分布 |
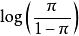 |
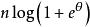 |
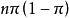 |
||
| 泊松分布 |
|||||
| 伽马分布 |
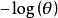 |

相关百科
-
截断二进制指数退避算法
2025-09-27 18:45:01 查看详情 -
比亚迪宋Plus 联手博世/采用分布式驱动
2025-09-27 18:45:01 查看详情 -
比亚迪海洋系轿车最新谍照 联手博世/采用分布式驱动
2025-09-27 18:45:01 查看详情 -
比亚迪秦PLUS 联手博世/采用分布式驱动
2025-09-27 18:45:01 查看详情 -
比亚迪海豹正式开启预售 联手博世/采用分布式驱动
2025-09-27 18:45:01 查看详情 -
比亚迪秦PLUS内饰设计图曝光 联手博世/采用分布式驱动
2025-09-27 18:45:01 查看详情 -
nanosox空气分布系统
2025-09-27 18:45:01 查看详情 -
纤维织物空气分布系统
2025-09-27 18:45:01 查看详情


 求购
求购




