模糊推理

相关书籍　　 从不精确的前提集合中得出可能的不精确结论的推理过程，又称近似推理。在人的思维中，推理过程常常是近似的。例如，人们根据条件语句（假言）“若西红柿是红的”，则西红柿是熟的”和前提（直言）“西红柿非常红”，立即可得出结论“西红柿非常熟”。这种不精确的推理不可能用经典的二值逻辑或多值逻辑来完成。L.A.扎德于1975年首先提出模糊推理的合成规则和把条件语句“若x为A，则y为B”转换为模糊关系的规则。此后J.F.鲍德温和R.R.耶格尔等人又各自采用带有模糊真值的模糊逻辑而提出了不同于扎德的方法。

应用实例　　自1965年L．A．Zadeh提出模糊集的概念以来，关于模糊 系 统的研究得到了迅猛的发展，模糊控制技术被广泛应用于工业控制与家电产品的制造中，并取得了令人瞩目的成功。模糊推理是模糊控制的理论基础，虽然模糊推理已有大量的研究成果，但这些研究还没有一个可靠的逻辑基础。王国俊教授于1996年建立了模糊命题演算的形式系统L~*，之后在系统L~*的框架中，从语义上为模糊推理规则构建了逻辑基础。1999年又基于只。蕴涵算子提出了糊推理的全蕴涵三I算法，这是比Zadeh提出的如今在控制领域中广泛应用的CRI方法更为合理，逻辑基础更强的推理算法。

结构推理　　由于蕴涵算子的选取与模糊推理的效果密切相关，特别是互为伴随的三角模与蕴涵算子的研究对将模糊推理与模糊逻辑相结合具有重要而广泛的意义。目的就是基于互为伴随的三角模与蕴涵算子建立一种新的模糊命题演算的形式系统RL，使得两类重要的逻辑系统 L~*和BL逻辑都是它的扩张。在这种新的模糊逻辑中，从语构上为模糊推理三I算法构建逻辑基础，得到了模糊推理的 非模糊形式。这样，就将模糊推理的三I算法纳入到形式模糊逻辑的框架之中，模糊推理过程可转化为模糊逻辑中的形式演绎，从而也使模糊推理有了严格的逻辑基础。

1.1.1 精确思维的缺陷

迄今， 经典逻辑和精确数学的成功推动了精确科学的迅速发展; 精确科学的巨大成就也造成了人类对“精确”的顶礼膜拜。人们普遍认为精确总是好的， 科学理论和方法必定是精确的， 模糊理论和方法一概是非科学的。在相当长的历史时期， 这种对“精确”的崇拜和“模糊”的否定被当作一条不言自明的公理。毋庸置疑， 强调“精确性”的观点对科学技术的发展曾起到极大的推动作用。相信宇宙在本质上不是模糊的而是精确的， 不满足于近似的、模糊的方法， 力求创造新的方法， 以获得更为精确的结果， 这种信念一直是激励科学家不断创新的动力。科学家再次对“模糊性”进行反思也正是这种不懈追求的结果。

富有批判精神的学者开始意识到， 以二值逻辑为基础的精确理论和方法是适应经典物理等∀ 精确科学# 的需要而发展起来的， 不可能不带有这些学科固有的局限性。在传统逻辑推理过程中， 首先要求概念是明确的， 而在现实世界， 尤其是人文、社会科学中的许多概念是没有明确类属边界的， 由此而涉及到的判断和推理也往往具有似然性， 所以需要引入新的理论和方法。

1.1.2 逻辑推理与模糊性

古典形式逻辑和现代数理逻辑都是精确的二值逻辑， 它们只适用于研究精确事物和现象。如果用这种∀ 非此即彼# 的逻辑来处理模糊对象， 就不得不将所处理的对象简化， 舍弃对象固有的模糊性， 在本来没有界限的对象之间人为地划定界限， 变模糊关系为清晰关系， 以便逻辑地形式化， 并由传统推理工具加以处理。然而， 人为地划定界限是对来相互联系着的事物性质的一种歪曲， 特别是在界限附近， 这种描述的失真性更为明显。当研究的对象相当复杂时， 这种处理方法就根本不适用了。罗素早在1923 年就指出: 传统逻辑通常假定所使用的符号是精确的， 因此， 它不适用于尘世生活， 而仅适用于想象中的天国。

科学的方法首先应当是有意义的， 对精确的盲目崇拜是建立在这样一条假设上的: 精确性和有意义性总是一致的， 越精确就越有意义。事实表明， 人类认识一旦进入层次复杂的客体， 就不得不

借助简化和抽象的手段来达到认识精确的目的， 而这样做可能导致更不精确的结果。这就是说， 把复杂的模糊事物人为地精确化， 势必降低所用方法的有意义性。查德将复杂性与精确性之间的矛盾概括为不相容原理( 或互克原理) : 当系统的复杂性增大时， 我们对系统特性的精确而有意义的描述能力将相应降低， 在达到一定的阈值时， 精确性和有意义性将相互排斥。

人类思维活动有两个显著的特点， 一是通过直觉与严格性的有机结合， 可以进行整体的、多方位的思考， 因而往往具有模糊性; 二是其推理过程具有逻辑有序的特征， 因而又应该是形式化的。以现代数理逻辑为基础的计算机科学在对精确问题的形式化方面取得了史无前例的成果， 但对模糊事物的处理就显得乏力了。现代科学形式化的困难， 终于把人们从片面追求精确思维的梦幻中唤醒。其实，每一个逻辑体系都基于一定的公理假设， 而这些假设的合理性是相对的。不承认中介的二值逻辑是伴随着精确数学、适应 精确科学 的需要而发展起来的，因而带有这些科学固有的局限性。由波兰的卢卡西维茨( J Lukasiew icz) 和美国的帕斯特( E L Post ) 等人建立起来的多值逻辑否定了真值的两极性， 在一定程度上承认了真值的中介过渡性。但是，多值逻辑局限于用穷举中介的方法承认过渡性，把中介看成彼此独立、界限分明的对象，不承认不同中介之间的相互渗透。因此， 多值逻辑实际上仍然是一种精确逻辑， 它也不可能从本质上把握模糊性。模糊性是指事物在性态和类属方面的亦此亦彼性， 即中介过渡性， 它是大多数人文系统固有的特性。从辩证的观点看， 亦此亦彼性包括着固有的特性。以下两层含义：

( 1) 两极对立的不充分性：一切两极对立都有中介，对立的两极通过中介而相互联系、相互转化。对于中介不明显的两级对立，略去中介，在非此即彼的意义上考察两极对立是可行的。而且对于明晰事物，只有这种非此即彼的模式才能更深刻、更正确地反映事物的本质。但在模糊事物中，对立的两极相互渗透、相互贯通， 呈现出一系列中介过渡状态。

（2) 自身同一的相对性：任何具体的同一性都是相对的，其中包含着差异和变化， 因而呈现出一定的不确定性。被人的思维视为同一的事物，基本上都是某种对象类，其中的不同对象属于该类的资格程度仍有一定差异， 只是这种差异限制在一定的范围内， 因而被近似地看作自身同一的。对于明晰事物， 同一中包含的差异很小，可以忽略；对于模糊事物， 就要通过研究这种差异和变化来把握事物自身的同一性。

模糊性同时表征上述两种性质， 可见它是反映事物本质的极为深刻的属性。辩证法认为，不同质的矛盾只有用不同质的方法才能得到解决。一般来说，人文社会系统和机械系统、模糊逻辑关系和精确逻辑关系之间有很大差别， 所以需要建立新的科确逻辑关系之间有很大差别，所以需要建立新的科学方法，以适应科学发展的需要。

在这种情况下，曾出现过一些实用近似推理方法，如可信度方法和D—S证据推理方法等。然而，从本质上说， 这些方法都是概率方法。众所周知，概率论是研究随机性的， 而随机性把握的仅仅是事物出现条件的不确定性， 还没有达到对人类思维机制中最本质的不确定性和模糊性的把握。

1.2 模糊推理理论研究的进展

逻辑学家对模糊性的研究始于罗素和布莱克( M. Black) ，但他们并没有提出新的理论。模糊集合论的诞生， 再次激起了人们研究模糊推理的热情1966 年，马里诺斯( P. N. Marinos) 在内部研究报告中首先提出了模糊逻辑的概念。1969年，哥冈( J. A. Gug uen) 研究了不精确概念的逻辑问题。在此以后，查德又相继提出了模糊限制词、语言变量和语言真值等重要概念，并以模糊集合论为基础建立了似然推理系统。该理论用模糊集合来刻划模糊概念，用近似推理规则进行模糊演绎。

查德的似然推理系统是对亚里士多德古典形式逻辑的拓展， 它基本上使用语义( 而不是通过语法) 进行推演， 其合理性主要由语义规定的无矛盾性来保证， 因此， 它不是经典数理逻辑那样的形式系统。从上世纪70 年代开始， 李( R. C. T. Lee) 和章( C. L. Chang) ，以及吉尔斯( R. Giles) 等先后提出了自己的模糊逻辑形式系统。这些成果是对经典数理逻辑的推广，它们在语法上与一阶谓词逻辑十分相似，但语义是不同的。因为模糊逻辑公式的真值不再是简单的0 ( 真) 或1 ( 假) ，而可能是[ 0，1] 区间上的任意实数。基于这些理论，美国的利夫埃瓦尔( R. A. LeFaivre) 于1974 年实现了第一个模糊推理语言。随后，美国、日本、英国、中国和法国等国家的科学家又相继实现了一系列风格不同的模糊推理语言和知识处理工具， 使模糊推理研究进入到崭新的阶段。模糊推理的另一个重要分支是模糊产生式( 规则) 系统，模糊产生式不同于模糊逻辑公式， 它的前件和后件之间不一定存在必然的逻辑关系，这种规则只被用作某种触发机制。

在专家系统中， “ if ……..then ……”规则并不总是表示逻辑公式， 它们可以看成是用于特殊情形的产生式规则或决策规则。于是“if….x 是A then B”可以解释为： “如果x 满足条件A， 则执行动作B”，这里B 可以是对知识库的更新，也可以是对某个过程的驱动，等等。模糊产生式系统与模糊逻辑系统的不同之处主要是，模糊产生式规则被视为元级规则，且模糊产生式系统的推理机是显式的，而模糊逻辑规则是通过自身隐含的推理机执行的。

1.3 模糊推理的研究领域和成果

1.3.1 模糊推理在模糊控制中的研究与应用

模糊推理应用最有效、最广泛的领域就是模糊控制，其方法被用于工业过程的控制以及新型家电产品的开发。并在这些领域出人意料的解决了传统控制理论无法解决的或难以解决的问题，并取得了一些令人信服的成效。传统的控制理论( 包括经典控制理论和现代控制理论) 是利用受控对象的数学模型( 即传递函数或状态空间模型) 对系统进行定量分析，而后设计控制策略。这种方法由于其本质的不相容性，当系统变得复杂时， 难以对其工作特性进行精确的描述。而且，这样的数学模型结构，也不利于表达和处理有关受控对象的一些不确定信息， 进而不便于利用人的经验知识、技巧和直觉推理， 所以难以对复杂系统进行有效的控制。近年来，随着智能控制理论研究的深入开展， 也由于其特有的对控制对象要求知识少、控制方法简单、实时性强、鲁棒性好等诸多优点， 模糊控制方法被广泛地应用于各个领域的复杂系统控制之中。然而对于多变量非线性的复杂系统的控制， 当前仍处于研究和探索之中，研究的主要问题包括模糊控制的稳定性、模糊模型及辩识、模糊最优控制、模糊自组织控制、模糊自适应控制、多模态模糊控制等 。

1.3.2 模糊推理在人工智能中的研究与应用

自然语言处理：自然语言与传统计算机语言的主要区别是具有模糊性。这种模糊性不仅表现在语音上，还表现在语法和语义上。例如，“高个子”、“ 歌星”、“红色”等词都是模糊的，而且这样的例子举不胜举。正如查德所说：“语句里的词汇大部分是模糊集合的名称，而不是非模糊集合的名称。”可见，模糊推理在自然语言处理 在自然语言中，出现在领域有着重要的应用价值。查德等设计并实现的通用可能性模糊关系语PRUF 是这一领域诸多成功范例中的典型代表。他们以模糊集合论和可能性理论为工具，研究自然语言的模糊性，创立了定量模糊语义学。PRUF通过四种翻译规则把自然语言语句转化为PRUF 表达式，进而用近似推理方法加以处理。该系统为自然语言处理和知识处理开辟了新的前景。

2.1 模糊集

模糊系统是建立在自然语言的基础上，而自然语言中常采用一些模糊的概念，如“温度偏高”、“压力偏大”等。如何描述这些模糊的概念，并对他们进行分析、推理，这正是模糊集和模糊逻辑所要解决的问题。

模糊集是一种边界不分明的集合，模糊集与普通集合既有区别又有联系。对于普通集合而言，任何一个元素要么属于该集合，要么不属于该集合，非此即彼，具有精确明了的边界；而对于模糊集合，一个元素可以是既属于该集合又不属于该集合，亦此亦彼，边界不分明或界限模糊。

建立在模糊集基础上的模糊逻辑，任何陈述或命题的真实性只是一定程度的真实性，与建立在普通集合基础上的布尔逻辑相比，模糊逻辑是一种广义化的逻辑。在布尔逻辑中，任何陈述或命题只有两种取值，即逻辑真和逻辑假，常用“l”表示逻辑真，“0”表示逻辑假。而在模糊逻辑中，陈述或命题的取值真和假(“1”和“0”)外，可取“0”与“l”之间的任何值。如0.75，即命题或陈述在多大程度上为真或假。例如“老人”这一概念，在普通集合中需要定义一个明确的边界，如60岁以上是老人，而在模糊集合中，老人的定义集合没有一个明确的边界，60岁以上是老人，58岁也属于老人，40岁在一定程度上也属于老人，只是他们属于老人这一集合的程度不同而已。

模糊性反映了事件的不确定性，但这种不确定性不同于随机性。随机性反映的是客观上的自然的不确定性，或事件发生的偶然性，而模糊性则反映了人们主观理解上的不确定性，即人们对有关事件定义或概念描述在语言意义理解上的不确定性。

2.2 模糊集的表示一隶属度函数

正确的确定隶属度函数，是运用模糊集合理论解决实际问题的基础。隶属度函数是对模糊概念的定量描述。我们遇到的模糊概念不胜枚举，然而对于能准确地反映了模糊概念的模糊集合的隶属度函数，却无法找到统一的模式。隶属度函数的确定过程，本质上说应该是客观的，但每个人对于同一模糊概念的认识理解又有差异，因此，隶属度函数的确定又带有主观性。一般是根据经验或统计进行确定，也可以由专家、权威给出。例如体操裁判的评分，尽管带有一定的主观性，但是却反映了裁判员们的大量丰富实际经验的综合结果。

对于同一个模糊概念，不同的人会建立不完全相同的隶属度函数，尽管形式不完全相同，只要能反映同一模糊概念，在解决和处理实际模糊信息的问题中仍然殊途同归。事实上，也不可能存在对任何问题对任何人都适用的确定隶属度函数的统一方法，因为模糊集合实质上是依赖于主观来描述客观事物的概念外延的模糊性。可以设想，如果有对每个人都适用的确定隶属度函数的方法，那么所谓“模糊性”就根本不存在了。

(1)隶属度函数的确定方法

从表面上看，隶属度似乎是主观的。实际上，模糊性的根源在于客观事物差异之间存在着中问过渡，存在着亦此亦彼的现象，但是，在亦此亦彼中依然存在着差异，依然可以相互比较。在上一层次中是亦此亦彼的东西，在下一层次中又可能是非此即彼的东西。这样，在客观上对隶属度进行了某种限定，使得不能主观任意地捏造隶属度。因此，隶属度函数也是具有可观规律的东西，不能主观任意确定。这里只介绍几种常用的隶属度函数的确定方法。

①模糊统计法：在有些情况下，隶属度函数可以通过模糊统计试验的方法来确定。但是这种方法的不足之处是工作量较大。

②例证法：例证法是zadeh在1972年提出的。主要思想是从已知有限个的

值，来估计论域U上的模糊子集爿的隶属度函数。

③专家经验法：根据专家的实际经验，确定隶属度函数的方法称专家经验法。

(2)常用的隶属度函数

在实际控制问题中，根据既能满足一般要求，又可简化计算的原则，通常选用的隶属度函数有三角形、半三角形、梯形、钟型(正态型)、矩形、Z型、S型和单点型等多种。

2.3 If then规则

最简单的if then规则的形式是：“如果x是A，则y是B”复合型if then规则的形式更多，例如：

“If 是A且x是B then y是c，否则z是D”

“If 是A且x是B且y是C then z是D”

“If 是A或x是B then y是c或z是D”

“If 是A且x是B then y是C且z是D”

这里的A、B、C、D分别是论域M、X、Y、Z中模糊集的语言值，if部分是前提或前件，then部分是结论或后件。解释if then规则包括以下三个过程：

①输入模糊化

确定出if then规则前提中每个命题或断言为真的程度(即隶属度)。

②应用模糊算子

如果规则的前提有几部分，则利用模糊算子可以确定出整个前提为真的程度(即整个前提的隶属度)。

③应用蕴含算子

由前提的隶属度和蕴含算子，可以确定出结论为真的程度(即结论的隶属度)。

2.4 模糊推理

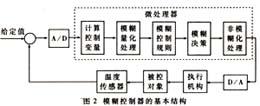
模糊推理是采用模糊逻辑由给定的输入到输出的映射过程。模糊推理包括五个方面：(如图2-1)

①输入变量模糊化，即把确定的输入转化为由隶属度描述的模糊集：

②在模糊规则的前件中应用模糊算予(与、或、非)；

③根据模糊蕴含运算由前提推断结论；

④合成每一个规则的结论部分，徭出总的结论；

⑤反模糊化，即把输出的模糊量转化为确定的输出。

(1)输入变量模糊化

输入变量是输入变量论域内的某一个确定的数，输入变量经模糊化后，变化

为由隶属度表示的0和l之间的某个数，模糊化常由隶属度函数或查表求得。

(2)应用模糊算子

输入变量经模糊化后，我们就知道每个规则前件中的每个命题被满足的程度。如果给定规则的前件中不止一个命题，则需要模糊算子获得该规则前件被满足的程度。模糊算子的输入是两个或多个输入变量经模糊化后得到的隶属度值，其输出是整个前件的隶属度，模糊逻辑算子可取71算子和协了．算子中的任意一个，常用的与算子有min(模糊交)和prod(代数积)，常用的或算子有max(模糊并)和probor(概率或)。Probor定义为：

) （2-1）

(3)模糊蕴含

模糊蕴含可以看作是一种模糊算子，其输入是规则的前件被满足的程度，输出是一个模糊集，规则“如果x是A，则y是B”表示了A与B之间的模糊蕴含关系，记为一B。在普通的形式逻辑中一B有严格的定义，但在模糊逻辑中一B不是普通逻辑的简单推广。很多人对此进行了研究，并提出了许多定义的方法。常见的有以下几种模糊蕴含关系的运算方法。

(4)模糊合成

模糊合成也是一种模糊算子。该算子的输入是每一个规则输出的模糊集，输出是这些模糊集经过合成后得到的一个综合输出模糊集。常用的模糊合成算子有(模糊并)、prob研(概率或)和sum(代数和)。

(5)反模糊化

反模糊化是把输出的模糊集化为确定数值的输出，常用的反模糊化的方法有以下五种：

①中心法

取输出模糊集的隶属度函数曲线与横坐标围成区域的中心或重心对应的论域元素值为输出值。

②二分法

取输出模糊集的隶属度函数曲线与横坐标轴围成区域的面积均分点对应的元素值为输出值。

③输出模糊集极大值的平均值。

④输出模糊集极大值的最大值。

⑤输出模糊集极大值的最小值。

2.5 模糊聚类

任何一门学科都需要通过分类来建立概念，也要通过分类来发现和总结规律，分类是建立和识别模型的重要基础和手段。所谓分类，就是将事物的总体分成若干类(子集)，使总体中的每一事物存在且仅存在一个类中。

聚类分析是按照一定的标准来鉴别事物之间的接近程度，并把彼此接近的事物归为一类。设数据X中含有n个样本，表示为以(k-1，2， n)，聚类问题是要把X区分为x中的c个子集2≤c≤x，要求相似的样本尽量在同一类，不相似的样本应在不同的类，聚类数c预先可能是不知道的。粗略地说，可以把聚类区分为三种：谱系聚类法、图论法以及目标函数法。

(1)谱系聚类法

谱系聚类法有两种类型：聚集法和分裂法。聚集法从n个只含单一个样本的聚类开始，然后逐步地将这些样本合并，聚集法的过程是从下往上。分裂法开始时把所有的样本考虑为同一类，法的过程是从上往下。聚集法的计算比较简单，但当样本数较多，用分裂法可省去许多复杂的计算。然后逐步分裂为多个类别，分裂而只需划分为很少的类别时，采用分裂法可省去许多复杂的计算。

(2)图论法

在图论法中，数据集的各个样本构成图的节点、联结节点，节点间边的加权系数反映了两个节点的相似性。各组节点间的连接度测度作为聚类准则。聚类方法通常在晟小生成树中去掉割边来形成多个子图。

(3)目标函数法

在目标函数法中，用目标函数来测度聚类的效果，最佳聚类对应于目标函数取得极值的情况。常用的准则是最小平方误差和。在matlab工具箱中用到的模糊聚类方法主要是模糊c均值聚类。模糊C均值聚类方法是通过对目标函数的迭代优化来获取数据集的模糊分类，目标函数为样本到聚类中心的距离平方和，然后采用目标函数进行聚类。

3.1 模糊模型建模过程

理想的模糊控制，必须建立在系统模糊模型辨识的基础上，也就是要进行模糊建模。一般来讲，建立模糊推理系统的标准方法，即通常所称为模糊建模的过程，有以下特征：

①模糊推理系统的规则结构使得它易于直接在建模过程中包容人类对目标系统的专门知识。也就是说，模糊建模可以利用其他建模方法不易或不能直接采用的领域知识。

②当拥有目标系统的输入输出时，传统的系统辨识技术可以用于模糊建模。换言之，数值数据的使用在模糊建模中与其在其他数学建模方法中一样，也起到了重要的作用。

如同常规的系统建模一样，模糊建模也包括两方面：系统的结构辨识和参数估计。结构辨识就是决定输入空间的划分和模糊规则。输入空间是由输入变量对应的隶属度函数来决定分割的，因此决定隶属度函数的形状、个数和模糊规则是结构辨识所要完成的任务。当模糊系统的模型结构确定以后，参数估计就是根据某种准则(如最小二乘准则)来决定模型中所有的参数。一般来说，结构辨识和参数辨识不能分开，通常是两个步骤交替反复数次才能获得最终模型。

(1)结构辨识

合适的模糊系统结构可以在模型的精度和泛化能力之间得到良好的折中，使随后的参数辨识得到简化，避免了参数学习时间过长和陷入局部极值点，所以结构辨识是模糊系统辨识中的核心问题。

常用的结构辨识方法有模糊树法、模糊聚类算法等。模糊树方法采用类似决策树的思想划分空间，具有较好的泛化性能，然而由于涉及到大量参数的辨识而增加了运算的复杂性；当对辨识对象的先验知识不足，只有大量输入输出数据时，聚类法被认为是最适宜的结构辨识方法

模糊聚类算法是一种基于训练数据的模糊系统结构辨识算法。该算法有效的前提是相似输入应产生相似的输出，一组相似的数据构成一个聚类。由此构成的模糊系统更适合逼近光滑函数，由于每一条模糊规则都具有局部模型逼近性，所以可以认为一个聚类对应一条规则。目前常用的离线聚类技术有：c均值聚类、模糊C均值聚类I嘲、山峰聚类方法和减法聚类方法等。聚类原则是聚类中的变化量最小化，聚类问的变化量最大化。

(2)参数辨识

参数辩识包括根据某种准则，对模糊模型参数进行辨识调整。对于参数的估计方法很多，常使用的有非线性最小二乘法、扩展卡尔曼滤波方法和梯度学习方法等。一般来讲，结构辨识和参数辨识是密不可分的，并且需要反复交替多次才能得到满足精度的模糊模型。

模糊辨识与传统的辨识方法在步骤和任务上大体相同，其不同之处在于它运用了模糊数学理论和不同的性能指标。模糊辨识作为一种新颖的辨识方法，具有独特的优越性：

①能有效的辨识复杂或病态结构的系统；

②能有效的辨识具有大时延、时变、多输入单输出的非线性系统；

③可以辨识性能优良的人类控制器；

④可以得到被控对象的定性与定量相结合的模型。

3.2 非线性系统的T-S模糊模型

T．S模型Takagi和sugeno于1985年提出的。它是一种本质非线性模型，

适用于表达复杂系统的动态模型。不失一般性，我们考虑具有埘个输入，单个输出的非线性系统的离散时间模型:

(3-1)

其中g是某种非线性映射函数，(f=l，2，⋯m)是系统t时刻以前的输入或者输出。MIMO系统可以看成是多个MISo系统，则g(力可以由，l条模糊规则组成的模糊逻辑系统来逼近。其中第均；模糊规则的形式为式(3-1)。

(3-2)

式中， ， n是模糊规则的数量； ( ) 是输入变量； （ ）是结论参数 ， 是完备的、一致的模糊子集，其隶属度函数中的参数为前提参数。

假设给定一个广义输入向量( )，那么由诸规则的输 的加权平均即可求得系统K时刻总的输出

(3-3)

3.3 T-S模型的参数辨识

T_S模糊模型辨识通常分为结构辨识和参数辨识两个部分。结构辨识又分为前提结构辨识和结论结构辨识；参数辨识又分为前提参数辨识和结论参数辨识。

(1)前提参数辨识

前提参数的辨识是指对给定的一组输入输出数据，求取使性能指标达到最小值的前提参数。对于模糊集合选用小、中、大三个子集，他们的隶属函数均由分段直线所构成，其中直线的转折点A，p1，p2….p8均为前提参数。前提参数的辨识可采用解非线性规划问题的复合型方法寻求最优参数，性能指标选取误差平方的均方值，即：

(3-4)

其中多(t)为由辨识的模糊模型计算出的第k个采样时刻的输出值，N为总的采样次数，在辨识过程中，要注意以下两点：

①每个前提参数要满足相应前提变量的定义域要求：

②对于每个前提变量范围的划分，要满足在定义域内的任何前提变量都能有对应的模糊子空间，以保证辨识输出结果的确定性。

(2)前提结构辨识

前提结构的辨识是要确定前提中的具体输入变量，并对输入空间进行最优划分。设前提中的输入变量为 ，每一条规则表示的仅是一种局部输入输出关系，例如某条规则表示在 =小和 =大模糊子空间确定的关系为 。采用PER性能指标，对前提结构的辨识算法如下：

①辨识普通的线性模型，计算出它的性能指标PER(1)。

②把y划分为小和大两个模糊子空间，前提结构表示成两条规则。再辨识前提参数和结论参数，计算出相应的PER。然后b变量也作上述类似处理，从这m个模型结构中，确定出最小的PER(2)及对应的结构STR(2)，并设STR(2)的对应变量为x。

③ 将前提中的模糊子空间由两个增加至三个，一种方法是将x．本身划分为图3-3(b)所示的小中大三个模糊子空间；另一种方法是将其它前提变量工，放到STR(2)中，并将其范围划分为两个模糊子空间，于是就形成前提结构，根据所构成的每个前提结构，辨识有关参数，计算并选出最小的PER作为PRE(3)和STR(3)。

④ 类似于第③步，将新的前提结构模糊规则数量由(i=1)个增加到i个(i>3)，同样用两种方法构造新的前提结构，一是将STR(i=1)的前提变量划分为两个模糊子空间；二是在其中的某个子空间与所有的输入变量不关联的情况下，再增加一个新的变量，并将该模糊子空间划分为两个子空间。对于构成的每个前提结构，类似于第三步，求得最小的PER(i)和对应的STR(i)。

⑤检验辨识结果是否满足如下某项指标：

(a)PER(i)小于预定值；

(b)规则数目达到预定值；

(c) PER(i)-PER（i-1）/PER（i）< e，e是给定的小数。

如果满足要求，可得到最优性能指标为PER(i)，最佳结构为STR(i)并获

得相应的前提结构参数，辨识过程结束，否则返回④。

(3)结论参数的辨识

结论参数辨识目的是确定每条规则的结论方程式中的各项系数。在式(3.3)中，模型输出多可以写为称H为数据行向量，口为待辨识的参数向量，上角标T表示转置。当给定一组输入输出数据后，可以应用最小二乘法或其他辨识方法对参数口进行辨识，以确定最佳的结论参数。

(4)结论结构的辨识

结论结构的辨识目的是确定结论中的最佳输入变量，为此，式(3-5)可以写为如下的一般形式

（3-5）

其中 意义同前，

假设在 离散时刻上测得L组输入输出数据（ ）应用多元线性逐步回归原理，对所有自变量分别进行F检验，就确定了结论的结构。

4.1 仿真软件简介

MATLAB 软件是Mathworks 公司于1982 年推出的一套用于数学建模的高性能工具软件， 是当今国际上最流行的软件之一。它集数值分析、矩阵运算、信号处理和图形显示于一体， 为用户进行数据运算和数据分析提供了强有力的工具， 从而大大简化了用户的编程工作量。随着模糊逻辑在自动控制领域的成功应用， 尤其是模糊控制的迅速推广应用， 使得Math Works 公司在其MATLAB 版中添加了Fuzzy Logic 工具箱， 提供了GUI ( 图形用户界面) 编辑函数，利用它用户可以更直接迅速地生成系统。本文主要介绍应用MATLAB 工具箱实现非线性系统的模糊建模方法及仿真， 并验证它的准确性。

4.2 设计原理

模糊通常是指利用模糊系统来逼近未知系统的非线性动态， 对一般线性系统而言， 用经典方法即用传递函数来描述输入输出间的关系， 而对非线性系统就显得非常困难， 在此研究领域里， Zadeh 首先提出模糊建模的思想， 从而使模糊建模作为模糊系统研究中的一个关键问题而受到人们的关注。在实际应用中， 非线性函数建模方法有很多， 在MATLAB模糊控制工具箱中， 就提出了基于Sugeno 模型的模糊神经网络实现方法， 而与此相应， 学者Jang- Sugeno 提出了与一阶Sugeno 模糊推理系统功能相同的基于自适应网络的模糊推理系统( ANFIS) ，此类系统是最适合模糊建模。

对ANFIS( 即Sugeno 型) 模糊推理系统， 其推理规定后项结论中的输出变量的隶属函数只能是关于输入线性或是常值函数， 若为线性函数则称为一阶系统， 若输出为常值函数，则称为0 阶系统， 本质就是从模糊集到常数集或线性集的映射。它的典型模糊规则有以下形式:

if x is A and y is B then z= k ( 0 型系统)

if x is A and y is B then z= p* x+ q* y+ r ( Ñ型系统)

ANFIS结构可以分成五层：

第一层：计算输入的模糊隶属度

i=1,2 (4-1)

j=3,4 (4-2)

结束语

系统仿真建模的规范化及引入DLL 技术实现模型， 大大提高了系统仿真模型的可重用性、可扩展性和透明性。同时， 系统仿真模型管理系统的建立有效地提高了对模型的存储和管理， 为提高系统仿真效率提供了一种有效手段， 使系统仿真过程中通过定制、优选仿真模型， 为研究不同模型对仿真对抗系统性能的影响提供了可能。随着目前仿真规模的日益扩大化， 规范化仿真建模的工作仍值得我们继续研究， 同时在如何更好地优化系统中实体模型的实现方式， 完善模型管理的功能方面做进一步的研究和改进。