- 切伦科夫辐射

切伦科夫辐射
荣誉记录
1937年另两名俄国物理学家伊利亚·弗兰克和伊戈尔·塔姆成功地解释了契伦科夫辐射的成因,三人因此共同获得1958年的诺贝尔物理学奖。
物理学解释
根据狭义相对论,具有静质量的物体运动速度不可能超过真空中的光速c,而光在介质中的传播速度(群速度)是小于c的,例如在水(折射率n≈1.33)中光仅以0.75c的速度在传播。物体可以被加速到超过介电质中的光速,加速的来源可以是核反应或者是粒子加速器。当超过介电质中光速的粒子是带电时(通常是电子)并通过这样的介质时,契伦科夫辐射即会产生。
此外,要超过的光速是光的相速度而非群速度。透过采用周期性介质(periodic medium)的方法,光的相速度可以被大幅改变,甚至可以让契伦科夫辐射没有最小粒子速度的限制——此现象称为史密斯-柏塞尔效应(Smith-Purcell effect)。在更复杂的周期性介质中,例如光子晶体,可以得到各式各样的异常契伦科夫效应(anomalous Cherenkov effects),例如反向传播的辐射(在寻常契伦科夫辐射中,辐射和粒子速度呈一锐角)。
具体产生条件
和契伦科夫辐射类似的是超音速飞行器或子弹的音爆现象。由超音速物体产生的音波速度无法快到足以离开物体,因此波“堆积”了起来,形成了一个震波波前。类似的情形,快船超过水波速度时也会在水面上产生很大的弓形震波(bow shock)。
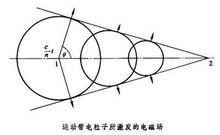 相同地,当一个带电的超光速粒子行经绝缘体,会产生光子振波。
相同地,当一个带电的超光速粒子行经绝缘体,会产生光子振波。
右图中,c是真空光速,n是介质的折射率,v是粒子速度(红色箭头),β=v/c。蓝色箭头则是发出的光。几何上,此二方向之角度关系为:
v=βc>c/n。
特性
契伦科夫辐射的总强度与入射带电粒子的速度成比例关系,另外粒子数量越多总强度也越强。与萤光或受激放射的电磁频谱具有特定频率的峰值的情形相异,契伦科夫辐射的频谱是呈连续性的。一个频率下的相对强度与该频率呈正比,也就是说在契伦科夫辐射,高频率(短波长)会有较强的强度。这解释了为何可见光波段部分的契伦科夫辐射看起来呈亮蓝色。实际上,多数契伦科夫辐射是在紫外线波段——当带电粒子被更充足地加速后,才会使可见光波段变得明显而得见;人眼感光最敏锐的波段是绿色光(平均为555纳米),对于蓝色光到紫色光的感应度则相当低。
如同音爆的情形一般,震波椎的角度与波源速度呈反比,在契伦科夫辐射也是如此。因此,观测到的入射角可以用来计算产生契伦科夫辐射的带电粒子的方向及速度。 契伦科夫辐射的总强度与入射带电粒子的速度成比例关系,另外粒子数量越多总强度也越强。
应用
切伦科夫辐射并非介质中运动的粒子(或物体)本身发出的辐射,而是介质中的极化电流发出的。在粒子物理学中切伦科夫辐射是一项非常重要的研究手段。例如Belle 实验的契伦科夫计数器,以及研究微中子震荡的超级神冈探测器,都是运作中的实际应用。从宇宙空间中进入地球大气层的某些高能粒子,运动速度接近光速,可以发出切伦科夫辐射。针对切伦科夫辐射设计出的契伦科夫探测器可以检测切伦科夫辐射的强度和方位,从而探测出高能粒子。在微中子研究相关的实验中,都有广泛的利用。

-
亚历山大·达尼洛维奇·缅什科夫
2025-09-20 10:43:27 查看详情


 求购
求购










