一元二次多项式

一元二次方程的求根公式是一种重要的数学公式，指用其系数表出其解的式子，复系数一元二次方程ax2+bx+c=0(a≠0)的求根公式为

式中Δ=b2-4ac称为一元二次方程的判别式。对于实系数一元二次方程，求根公式可具体地写成：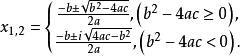

这组公式中前一公式用于在方程的判别式非负时求出实根，后一公式用于在方程的判别式为负时求出两个共轭虚根。当方程是有理系数一元二次方程，且要求有有理数根时，只有当Δ=b²-4ac是一个有理数的完全平方数才有解.这时求根公式仍为

其中q/p为既约分数，且(q/p)²=b²-4ac，当方程是整系数方程又要求整根时，仍可利用有理数方程求有理根的公式，但要

是整数时方程才有解。

公元前两千年左右，古巴比伦人的泥板文书中就已经记载有一元二次方程的知识：求出一个数使它与它的倒数之和为已知数。用现代记法可表示为

从这个方程可得出x²-bx+1=0，巴比伦人做出

再做出

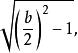然后得出解答

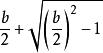及

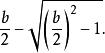由此可知，巴比伦人知道一元二次方程的求根公式，但他们当时并不认识负数，对负根是不予理会的。

埃及的草纸文书中也有简单一元二次方程ax2=b的记载。丢番图(Diophantus)也承认二次方程的一个正根，即使两根都是正的也只取一个.婆罗摩笈多(Brahmagupta)在公元628年写成的《婆罗摩修正体系》中，得到二次方程x2+px-q=0的一个求根公式

阿尔·花拉子米(M.ibn M.al-Khowārizmī)于826年给出二次方程的几种特殊解法，并第一次给出二次方程的一般解法，承认方程有两个根，还允许无理根的存在，只是还未认识虚根。复数根的应用到16世纪意大利的数学家们解三次方程时才开始，韦达(F.Viete)已经知道一元二次方程在复数范围内恒有解，并且给出了根与系数的关系。在中国，《九章算术》中已有了一元二次方程的内容，“勾股”第20题是通过方程x2+34x-7100=0的正根而解决的^[1]。

一元二次多项式根的对称多项式定理是对称多项式基本定理的特例，一元二次多项式x2+px+q的两根的任何对称多项式都能惟一地表成p与q的多项式形式。这个结论称为一元二次多项式根的对称多项式定理^[1]。

两个二次多项式f(x) = ax²+bx+c(a≠0)及f1(x)=a1x²+ b1x + c1(a1≠0)有公共零点(即至少有一个公共根)，必须而且只须条件

(ac1-ca1)-(ab1-ba1)(bc1-cb1)=0

成立。上述等式左端的表达式叫做多项式f及f1的结式，记作R(f，f1)^[2]。