

酉群



酉群

目录导航

性质

因为酉矩阵的行列式是模长1复数，行列式给出了一个群同态

这个同态的核是行列式为单位的酉矩阵集合，这个子群称为特殊酉群，记作SU(n)。我们有李群的短正合列：

。

这个短正合列分裂，故U(n)可以写成SU(n)与U(1)的半直积。这里U(1)是U(n)中由,1,1,...,1)形式的矩阵组成的子群。

酉群U(n)对n > 1是非交换的。U(n)的中心是数量矩阵λI，这里λ ∈ U(1)。这由舒尔引理得来。这样中心同构于U(1)。因为U(n)的中心是一个1维阿贝尔正规子群，酉群不是半单的。

拓扑

酉群U(n)作为M_n(C)的子集赋予相对拓扑，M_n(C)是所有n×n复矩阵集合，本身同构于2n²维欧几里得空间。

作为一个拓扑空间，U(n)是紧连通空间。因为U(n)是M_n(C)的一个有界闭子集，然后海涅-博雷尔定理可知紧性。欲证U(n)是连通的，回忆到任何酉矩阵A能被另一个酉矩阵S 对角化。任何对角酉矩阵的对角线上都是绝对值为1的复数。从而我们可以写成

。

U(n)中从单位到A的一条道路由

给出。

酉群不是单连通的；对所有n，U(n)的基本群是无限循环群

。

第一个酉群U(1)是一个拓扑圆周，熟知其有同构于Z的基本群，包含映射在上是同构（其商是斯蒂弗尔流形）。

行列式映射诱导了基本群的同构，分裂映射诱导其逆。

三选二性质

酉群是正交群、辛群与复数群的3重交集：

从而一个酉结构可以视为一个正交结构、复结构与辛结构，他们要求是“一致的”（意思是说：复结构与辛形式使用同样的J，且J是正交的；取定一个J将所有群写成矩阵群便确保了一致性）。

事实上，它是这三个中任何两个的交集；从而一个一致的正交与复结构导致了一个辛结构，如此等等。

在方程的层次上，这可以由下面看出

辛：

复：

正交：

任何两个方程蕴含第三个。

在形式的层次上，这可从埃尔米特形式分解为实部与虚部看出：实部是对称的（或正交），虚部是斜正交（辛）——他们由复结构联系（这便是一致性）。在一个殆凯勒流形上，可以将这个分解写成，这里h是埃尔米特形式，g是黎曼度量，i是殆复结构，而是殆辛结构。

从李群的观点来看，这可部分地解释如下：是的极大紧子群，而是与的极大紧子群。从而交集或是这些群的极大紧子群，即。从这个观点来看，意料之外的是交集。

特殊酉群与射影酉群

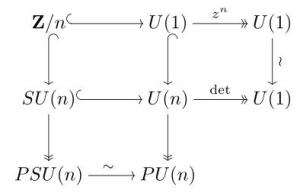
就像正交群有子群特殊正交群与商群射影正交群PO(n)，以及子商群射影特殊正交群；酉群也有关联的特殊酉群SU(n)，射影酉群PU(n)，以及射影特殊酉群PSU(n)。他们的关系如左所示的交换图表；特别地，两个射影群相等：。

上面对经典酉群成立（复数上），对有限域，可以类似地得到特殊酉群与射影酉群，但是一般地。

G-结构：殆埃米尔特

用G-结构的语言来说，一个具有-结构的流形是一个殆埃米尔特流形。

推广

从李群的观点来看，典型酉群是斯坦伯格群的实形式，后者是由一般线性群的“图表自同构”（翻转Dynkin diagram ，对应于转置逆）与扩张的域同构（即复共轭）的复合得到的代数群。两个自同构都是代数群的自同构，阶数为2，可交换，酉群作为代数群是乘积自同构的不动点。典型酉群是这个群的实形式，对应于标准埃尔米特形式，它是正定的。

这可从几个方面推广：

推广到其它埃尔米特形式得到了不定酉群；

域扩张可用任何2阶可分代数取代，最特别地是一个2阶有限域扩张；

推广到其它图表得出李型群，即其它斯坦伯格群（以及）Suzuki-Ree群；

考虑一个推广的酉群作为代数群，可取它的点在不同的代数上。

不定形式

类似于不定正交群，给定一个不必正定（但一般取为非退化）的埃尔米特形式，考虑保持这个形式的变换，我们可以定义不定酉群。这里我们在复向量空间上考虑问题。

给定复向量空间上的一个埃尔米特形式，酉群是保持这个形式的变换群：变换使得，对所有。写成矩阵，设这个形式用矩阵表示，这便是说。

就像实数上的对称形式，埃尔米特形式由符号确定，所有都是酉合同于对角线上个元素为1，个的对角矩阵。非退化假设等价于。在一组标准基下，这代表二次形式：

作为对称形式是：

得出的群记为。

有限群

在个元素的有限域上，有一个惟一的2阶扩张域，带有2阶自同构（弗罗贝尼乌斯自同构的次幂）。这使得我们可以定义上一个向量空间上的埃尔米特形式，是一个-双线性映射使得以及对。另外，有限域上向量空间的所有非退化埃尔米特形式都酉合同与用恒同矩阵表示的标准形式。这便是说，任何埃尔米特形式酉等价于

这里表示在-维空间的某个特定-基下的坐标（Grove 2002，Thm. 10.3）。

从而我们对扩张可以定义一个（惟一的）维酉群，记作或（取决于作者的习惯）。酉群中矩阵的行列式为1的子群称为特殊酉群，记作或。为方便起见，本文使用写法。的中心的阶数为由为酉数量矩阵组成，这便是所有矩阵，这里。特殊酉群的中心的阶数为，由那些阶数整除的酉数量矩阵组成。酉群除以中心的商称为射影酉群，，特殊酉群除以中心是射影特殊酉群。在大多数情形（与），是完全群而是有限单群（Grove 2002，Thm. 11.22 and 11.26）。