- 四分位距

四分位距
定义
四分位距通常是用来构建箱形图,以及对概率分布的简要图表概述。对一个对称性分布数据(其中位数必然等于第三四分位数与第一四分位数的算术平均数),二分之一的四分差等于绝对中位差(MAD)。中位数是集中趋势的反映。
公式:IQR = Q3 − Q1
示例
图表中数据
| 数列 | 参数 | 四分差 |
| 1 | 102 | |
| 2 | 104 | |
| 3 | 105 | Q1 |
| 4 | 107 | |
| 5 | 108 | |
| 6 | 109 | Q2 (中位数) |
| 7 | 110 | |
| 8 | 112 | |
| 9 | 115 | Q3 |
| 10 | 118 | |
| 11 | 118 |
从这个表格中,我们可以算出四分差的距离为 115− 105 = 10。
箱形图中数据
| 数列 | 参数 | 四分差 |
| 1 | 102 | |
| 2 | 104 | |
| 3 | 105 | Q1 |
| 4 | 107 | |
| 5 | 108 | |
| 6 | 109 | Q2 (中位数) |
| 7 | 110 | |
| 8 | 112 | |
| 9 | 115 | Q3 |
| 10 | 118 | |
| 11 | 118 |
用途
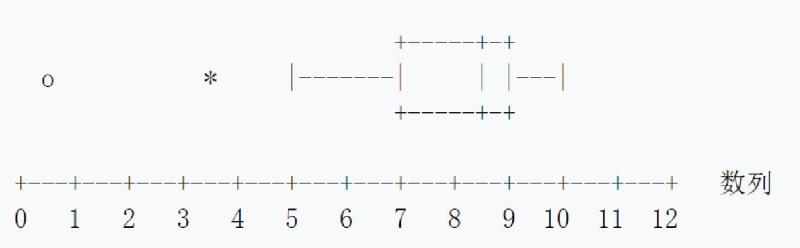 图1.箱形图中的数据
图1.箱形图中的数据
从该图中我们可算出:
第一四分位数 (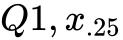 ) = 7;
) = 7;
中位数 (第二四分位数) (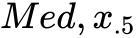 ) = 8.5;
) = 8.5;
第三四分位数 (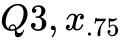 ) = 9;
) = 9;
四分位距![]() =Q3-Q1=2};
=Q3-Q1=2};
四分位差![]() =(Q3-Q1)/2=1}。
=(Q3-Q1)/2=1}。
相关条目
- 与总范围不同,四分位数范围的分解点为25%,因此通常优选总范围。
- IQR用于构建箱形图,概率分布的简单图形表示。
- 对于对称分布(其中中位数等于midhinge,第一和第三四分位数的平均值),IQR的一半等于中值绝对偏差(MAD)。
- 中位数是集中趋势的相应度量。
- IQR可以用来识别异常值。
- 四分位数偏差或半四分位数范围被定义为IQR的一半。
四分位数
百分位数
四分位数(Quartile)是统计学中分位数的一种,即把所有数值由小到大排列并分成四等份,处于三个分割点位置的数值就是四分位数。
- 第一四分位数(Q1),又称“较小四分位数”,等于该样本中所有数值由小到大排列后第25%的数字。
- 第二四分位数(Q2),又称“中位数”,等于该样本中所有数值由小到大排列后第50%的数字。
- 第三四分位数(Q3),又称“较大四分位数”,等于该样本中所有数值由小到大排列后第75%的数字。
第三四分位数与第一四分位数的差距又称四分位距(InterQuartile Range, IQR)。

相关百科
-
翼之影 · 四分休止符
2025-10-31 14:24:02 查看详情 -
走过流行音乐的四分之一世纪
2025-10-31 14:24:02 查看详情


 求购
求购








