- 三角恒等变换

三角恒等变换
基础等式
sin²a+cos²a=1
 三角恒等变换 sina/cosa=tana
三角恒等变换 sina/cosa=tana
两角和差
![]()
![]()
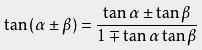
倍角公式
二倍角
 三角恒等变换 sin2α = 2cosαsinα = 2tanα / (1 + tan²α)
三角恒等变换 sin2α = 2cosαsinα = 2tanα / (1 + tan²α)
cos2α = cos²α-sin²α=1-2sin²α=2cos²α-1
tan2α = 2tanα/[1 - (tanα)²]
二倍角变式
sin2α = sin^2(α + π/4) - cos^2(α + π/4) = 2sin^2(a + π/4) - 1 = 1 - 2cos^2(α + π/4);
cos2α = 2sin(α + π/4)cos(α + π/4)
三倍角
sin3α=3sinα-4sin³α
cos3α=4cos³α-3cosα
tan3α=(3tanα-tan³α)/(1-3tan²α)
sin3α=4sinα×sin(π/3-α)sin(π/3+α)
cos3α=4cosα×cos(π/3-α)cos(π/3+α)
tan3α=tanα×tan(π/3-α)tan(π/3+α)
n倍角
根据欧拉公式(cos θ+i·sin θ)^n=cos nθ+i·sin nθ (注:sin θ前的 i 是虚数单位,即-1开方)
将左边用二项式定理展开分别整理实部和虚部可以得到下面两组公式
sin(nα)=ncos^(n-1)α·sinα-C(n,3)cos^(n-3)α·sin^3α+C(n,5)cos^(n-5)α·sin^5α-…
cos(nα)=cos^nα-C(n,2)cos^(n-2)α·sin^2α+C(n,4)cos^(n-4)α·sin^4α
辅助角
Asinα+Bcosα=√(A^2+B^2)sin[α+arctan(B/A)]
Asinα+Bcosα=√(A^2+B^2)cos[α-arctan(A/B)]
半角公式
sin(α/2)=±√[(1-cosα)/2]
cos(α/2)=±√[(1+cosα)/2]
tan(α/2)=±√[(1-cosα)/(1+cosα)]=sinα/(1+cosα)=(1-cosα)/sinα=cscα-cotα
cot(α/2)=±√[(1+cosα)/(1-cosα)]=(1+cosα)/sinα=sinα/(1-cosα)=cscα+cotα
sec(α/2)=±√[(2secα/(secα+1)]
csc(α/2)=±√[(2secα/(secα-1)]
诱导公式
 三角恒等变换(3)kπ+a
三角恒等变换(3)kπ+a
sin(2kπ+α)=sinα
cos(2kπ+α)=cosα
tan(kπ+α)=tanα
cot(kπ+α)=cotα
sec(2kπ+α)=secα
csc(2kπ+α)=cscα
sin(π+α)=-sinα
cos(π+α)=-cosα
tan(π+α)=tanα
cot(π+α)=cotα
sec(π+α)=-secα
csc(π+α)=-cscα
-a
sin(-α)=-sinα
cos(-α)=cosα
tan(-α)=-tanα
cot(-α)=-cotα
sec(-α)=secα
csc(-α)=-cscα
π-a
sin(π-α)=sinα
cos(π-α)=-cosα
tan(π-α)=-tanα
cot(π-α)=-cotα
sec(π-α)=-secα
csc(π-α)=cscα
π/2±a
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
tan(π/2+α)=-cotα
cot(π/2+α)=-tanα
sec(π/2+α)=-cscα
csc(π/2+α)=secα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
tan(π/2-α)=cotα
cot(π/2-α)=tanα
sec(π/2-α)=cscα
csc(π/2-α)=secα
3π/2±a
sin(3π/2+α)=-cosα
cos(3π/2+α)=sinα
tan(3π/2+α)=-cotα
cot(3π/2+α)=-tanα
sec(3π/2+α)=cscα
csc(3π/2+α)=-secα
sin(3π/2-α)=-cosα
cos(3π/2-α)=-sinα
tan(3π/2-α)=cotα
cot(3π/2-α)=tanα
sec(3π/2-α)=-cscα
csc(3π/2-α)=-secα
恒等变形
 数学概念(3)tan(a+π/4)=(tan a+1)/(1-tan a)
数学概念(3)tan(a+π/4)=(tan a+1)/(1-tan a)
tan(a-π/4)=(tan a-1)/(1+tan a)
asinx+bcosx=[√(a²+b²)]{[a/√(a²+b²)]sinx+[b/√(a²+b²)]cosx}=[√(a²+b²)]sin(x+y)【辅助角公式,其中tan y=b/a,或者说sinx=b/[√(a²+b²)],cosx=a/[√(a²+b²)]】
万能代换
半角的 正弦、余弦 和正切公式( 降幂扩角公式)
积化和差
sinα·cosβ=(1/2)[sin(α+β)+sin(α-β)]
cosα·sinβ=(1/2)[sin(α+β)-sin(α-β)]
cosα·cosβ=(1/2)[cos(α+β)+cos(α-β)]
sinα·sinβ= -(1/2)[cos(α+β)-cos(α-β)](注:留意最前面是负号)
和差化积
![]()
这里应该是cos((α-+β)/2)
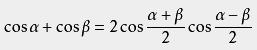
![]()
内角公式
设A,B,C是三角形的三个 内角
sinA+sinB+sinC=4cos(A/2)cos(B/2)cos(C/2)
cosA+cosB+cosC=1+4sin(A/2)sin(B/2)sin(C/2)
tanA+tanB+tanC=tanAtanBtanC
cot(A/2)+cot(B/2)+cot(C/2)=cot(A/2)cot(B/2)cot(C/2)
tan(A/2)tan(B/2)+tan(B/2)tan(C/2)+tan(C/2)tan(A/2)=1
cotAcotB+cotBcotC+cotCcotA=1
(cosA)^2+(cosB)^2+(cosC)^2+2cosAcosBcosC=1
sin2A+sin2B+sin2C=4sinAsinBsinC
降幂公式
![]()
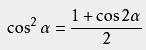
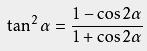
证明方法
首先,在三角形ABC中,角A,B,C所对边分别为a,b,c若A,B均为锐角,则 在三角形ABC中,过C作AB边垂线交AB于D 由CD=asinB=bsinA( 做另两边的垂线,同理)可证明正弦定理:a/sinA=b/sinB=c/sinC于是有:AD+BD=c AD=bcosA,BD=acosB AD+BD=c代入正弦定理,可得sinC=sin(180-C)=sin(A+B)=sinAcosB+sinBcosA 即在A,B均为锐角的情况下,可证明正 弦和的公式。利用正弦和 余弦的定义及周期 性,可证明该公式对 任意角成立。于是有 cos(A+B)=sin(90-A-B)=sin(90-A)cos(-B)+cos(90-A)sin(-B)=cosAcosB-sinAsinB
由此求得以上全部公式

-
长江三角洲地区区域规划
2025-11-03 22:28:17 查看详情


 求购
求购










