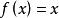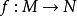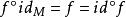- 恒等函数

恒等函数
定义
设为一集合,于上的恒等函数被定义于一具有定义域和陪域的函数,其对任一内的元素,会有的关系。于上的恒等函数通常标记为或。
代数性质
设为任一函数,则会有其中""为函数复合)。特别地是,会是所有由至的函数所组成之幺半群的单位元。,
因为幺半群的单位元是唯一的,可以以上的单位元来替代其恒等函数的定义。此一定义广义化成了于范畴论中恒等态射的概念,其中的自同态并不必然要是个函数。
恒等函数![]() 是
是![]() 到
到![]() 函数,即
函数,即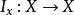 ,称之为恒等函数。显然,对
,称之为恒等函数。显然,对![]() ,有
,有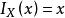 。
。
例子
1) 于正整数上的恒等函数为一数论中的完全积性函数。
2) 在一![]() 维向量空间内,恒等函数表示成单位矩阵
维向量空间内,恒等函数表示成单位矩阵![]() ,不论其基为何。
,不论其基为何。
3) 在一度量空间,恒等函数很当然地为等距同构。一无任何对称的物件会有一对称群,即只包含这个恒等函数的平凡群![]() 。
。

相关百科
-
1641函数信号发生器
2025-09-20 07:11:14 查看详情


 求购
求购