- 伪随机序列

伪随机序列
伪随机序列理论的发展历史
伪随机序列的理论与应用研究大体上可以分成三个阶段:(1)纯粹理论研究阶段 (1948年以前);(2)m序列研究的黄金阶段(1948-1969); (3)非线性生成器的研究阶段 (1969-)。
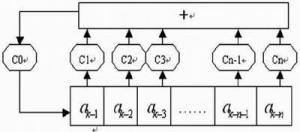 伪随机序列产生原理图1948年以前,学者们研究伪随机序列的理论仅仅是因为其优美的数学结构。最早的研究可以追溯到1894年,作为一个组合问题来研究所谓的De Bruijn序列;上世纪30年代,环上的线性递归序列则成为人们的研究重点.
伪随机序列产生原理图1948年以前,学者们研究伪随机序列的理论仅仅是因为其优美的数学结构。最早的研究可以追溯到1894年,作为一个组合问题来研究所谓的De Bruijn序列;上世纪30年代,环上的线性递归序列则成为人们的研究重点.
1948年Shannon信息论诞生后,这种情况得到了改变。伪随机序列己经被广泛的应用在通信以及密码学等重要的技术领域。Shannon证明了“一次一密”是无条件安全的,无条件保密的密码体制要求进行保密通信的密钥量至少与明文量一样大。因此在此后的一段时间内,学者们一直致力于研究具有足够长周期的伪随机序列。如何产生这样的序列是20世纪50年代早期的研究热点。线性反馈移位寄存器 (LFSR)序列是这个时期研究最多的,因为一个n级LFSR可以产生周期为的最大长度序列,而且具有满足Golomb随机性假设的随机特性,通常称之为m序列。这段时期的研究奠定了LFSR序列的基本理论和一些经典结论。
但是,在1969年Massey发表了“移位寄存器综合与BCH译码”一文,引发了序列研究方向的根本性变革,从此伪随机序列的研究进入了构造非线性序列生成器的阶段。Berlekamp-Massey算法(简称B-M算法)指出:如果序列的线性复杂度为n,则只需要2n个连续比特就可以恢复出全部的序列。从这个结论可以看出m序列是一种“极差”的序列,它的线性复杂度太小,因而不能够直接用来做流密码系统的密钥流序列。从这里还可以看到仅仅靠Golomb的三个随机性假设来评测序列是不够的,还需要其它的一些指标。此后直到今天,密码学界的学者们一直在努力寻找构造“好”的伪随机序列的方法。
简介
 伪随机序列伪随机序列是具有某种随机特性的确定的序列。它们是由移位寄存器产生确定序列,然而他们却具有某种随机特性的随机序列。因为同样具有随机特性,无法从一个已经产生的序列的特性中判断是真随机序列还是伪随机序列,只能根据序列的产生办法来判断。伪随机序列系列具有良好的随机性和接近于白噪声的相关函数,并且有预先的可确定性和可重复性。这些特性使得伪随机序列得到了广泛的应用,特别是在CDMA系统中作为扩频码已成为CDMA技术中的关键问题。特性为序列中两种元素出现的个数大致相等。
伪随机序列伪随机序列是具有某种随机特性的确定的序列。它们是由移位寄存器产生确定序列,然而他们却具有某种随机特性的随机序列。因为同样具有随机特性,无法从一个已经产生的序列的特性中判断是真随机序列还是伪随机序列,只能根据序列的产生办法来判断。伪随机序列系列具有良好的随机性和接近于白噪声的相关函数,并且有预先的可确定性和可重复性。这些特性使得伪随机序列得到了广泛的应用,特别是在CDMA系统中作为扩频码已成为CDMA技术中的关键问题。特性为序列中两种元素出现的个数大致相等。
如果把n个元素连续出现叫做一个长度为n的元素游程,则序列中长度为n的元素游程比长度为n+1的元素游程多一倍。
序列元素间有确定关系存在,但具有与随机序列类似性质的一种特殊的离散信号形式,可表示为
…,ɑ-1,ɑ0,ɑ1,ɑ2,…
其中ɑi可取值0,1或1,-1;也可以取符号域GF(q)(见分组码)中的元素。前者叫二元序列,后者叫q元序列。但实用中最主要的还是前者。序列长度可以为有限,也可以为无穷。后者主要着重的是周期序列,即存在最小正整数夞,使对一切i有ɑp=ɑp+i,p为周期。
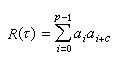 相关函数序列的各元素为相互独立且具有相同分布的随机变量时,称为随机序列。实际应用的主要是伪随机列。它指序列元素间有确定关系存在,但具有与随机序列类似的下列性质:①在有限长度或一周期内各元素个数相差不超过1,即接近等概率;②出现l个相同值或称l长游程的概率接近1/ql;③相关函数在τ=0时为p,τ厵0时不超过±1,式中p为序列的长度或周期。实际上有时将大体满足以上条件的序列也称为伪随机序列。
相关函数序列的各元素为相互独立且具有相同分布的随机变量时,称为随机序列。实际应用的主要是伪随机列。它指序列元素间有确定关系存在,但具有与随机序列类似的下列性质:①在有限长度或一周期内各元素个数相差不超过1,即接近等概率;②出现l个相同值或称l长游程的概率接近1/ql;③相关函数在τ=0时为p,τ厵0时不超过±1,式中p为序列的长度或周期。实际上有时将大体满足以上条件的序列也称为伪随机序列。
构造
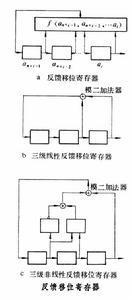
伪随机序列可用图中ɑ的反馈移位寄存器得到。图中f(ɑn+i-1,ɑn+i-2,…,ɑi)表示反馈函数。n级移位寄存器只能有2n(一般为qn)种状态, 故经一定时间后会回到原来的某一状态, 产生周期性输出, 若反馈函数的输出ɑn+i与各输入ɑn+i-1,…,ɑi间有线性关系存在,则为线性移位寄存器,否则为非线性移位寄存器。图中b和c分别是三级线性和非线性反馈移位寄存器。
对于线性移位寄存器序列有
ɑn+i=c0ɑn+i-1+c1ɑn+i-2+…+cn-1ɑi
(i=0,1,…)
![]() 相关函数它当初始值ɑ0,ɑ1,…,ɑn-1全为零时输出恒为零。除去这种全零状态外,它最多可能取遍所有2n-1个非零状态,故最大周期为2n-1。一般情况下周期是2n-1的因子。 周期达到2n-1的序列称为最长线性移位寄存器序列,简称M序列,图中b就是三级M序列,它的输出为…,0,0,1,0,1,1,1,…。M序列完全满足伪随机序列的三点要求,特别是它的相关函数为因而是典型的伪随机序列。
相关函数它当初始值ɑ0,ɑ1,…,ɑn-1全为零时输出恒为零。除去这种全零状态外,它最多可能取遍所有2n-1个非零状态,故最大周期为2n-1。一般情况下周期是2n-1的因子。 周期达到2n-1的序列称为最长线性移位寄存器序列,简称M序列,图中b就是三级M序列,它的输出为…,0,0,1,0,1,1,1,…。M序列完全满足伪随机序列的三点要求,特别是它的相关函数为因而是典型的伪随机序列。
M序列的周期一定是2n-1,实用上还需要有其他的周期,这可用非线性移位寄存器序列得到。n级非线性移位寄存器序列的周期不大于2n,达到2n的序列称M序列。
一般M序列的相关函数不完全接近冲激函数。接近冲激函数的非线性移位寄存器序列主要有二次剩余或称勒让德序列,简称L序列,以及孪生素数序列。两者的相关函数均如式(3)。L序列是周期为形如4k-1的素数时所构造的序列,k为自然数。前几个L序列的周期为3,7,11,19,23,…。当周期不超过任一大的正整数时,L序列的种类比M序列多得多。孪生素数序列是周期为k(k+2)的伪随机序列,在此k与k+2均为素数,前几个序列的周期为15,35,143,…。
序列族
应用中有关的全部序列叫序列族,且通常取周期相同的一族序列。既有良好的自相关特性又有良好的互相关特性的线性伪随机序列族,主要有戈尔德序列族和嵩忠雄序列族等。
戈尔德序列族是由适当选择的一对n级M序列线性组合构成,在此n呏1(mod 4)或n呏2(mod 4)。序列族中共有2n+1个序列,周期均为2n-1,两两之间的互相关函数最大值为2【(n+2)-2】+1,此处【X】表示不超过x的最大整数。n为偶数时戈尔德序列的性能较差,而嵩忠雄序列却可达到最佳。后者由n级M序列和相应的n/2级M序列的线性组合构成。它的周期也是2n-1,但序列只有2个,互相关函数最大值是2+1。
伪随机序列研究现状
迄今为止,人们获得的伪随机序列仍主要是PC(相控)序列,移位寄存器序列(m和M序列),Gold序列,GMW序列,级联GMW序列,Kasami序列,Bent序列,No序列。
其中m序列是最有名和最简单的,也是研究的最透彻的序列。m序列还是研究其它序列的基础。它序列平衡,有最好的自相关特性,但互相关满足一定条件的族序列数很少(对于本原多项式的阶数小于等于13的m序列,互为优选对的序列数不多于6),且线性复杂度很小。M序列族序列数极其巨大(当寄存器级数等于6时,有226个序列)。但其生成困难,且其互相关特性目前知之甚少,一般很少用。Gold序列互相关函数为3值,序列部分平衡,有良好的相关特性,族序列数相对较大,但它有致命的弱点,线性复杂度很低,仅是相同长度的m序列的两倍,这制约了Gold序列的广泛应用,特别在抗干扰及密码学中的应用。GMW序列具有序列平衡,线性复杂度大,自相关性能好(同m序列)等优点。它是非线性序列,且数量比m序列多。作为单个序列GMW序列有优势,但一族GMW序列满足一定互相关条件的序列数很少。一般不用于多址通信作地址码。级联GMW序列平衡性和相关性同于GMW序列,族数比GMW序列多,一般情况下,线性复杂度比GMW序列大。Kasami序列分小集Kasami序列和大集Kasami序列。小集Kasami序列族序列数大,且互相关值达welch下界,大集Kasami序列族序列数非常大,互相关较小集Kasami序列为劣。它们都有共同的弱点,序列是不平衡的,线性复杂度不大(但比m, Gold序列稍大)。Bent序列是80年代初构造出来的,具有序列平衡,相关值达welch下界,族序列数多,线性复杂度大等优点。它在整个80年代,90年代大放光芒,也是目前综合性能最好的伪随机序列。但Bent序列构造较难,未有满足一定要求的快速算法。No序列是80年代末构造出来的一种新型伪随机序列,它的突出优点是线性复杂度很大,且相关值可达welch下界,族序列数多,但有序列不平衡的弱点。
m序列
m序列的定义
m序列[1]是最长线性反馈移存器序列的简称,它是由带线性反馈的移存器产生的周期最长的一种序列。
m序列的产生
扰码的目的是使短周期输入序列变为长周期的信道序列。从原则上看,就可以用将一个长周期序列叠加在输入序列上的方法来实现,并且叠加序列的周期越长越好。从理论上说,一个真正的随机(二进制)序列的“周期”是无限长的,但是,采用这种序列时在接收端将无法产生相同的序列与之同步。所以,人们就不得不企图用简单电路来产生尽量长的序列。同时随机噪声在通信技术中,首先是作为有损通信质量的因素受到人们重视的。信道中存在的随机噪声会使模拟信号产生失真,或使数字信号解调后出现误码;同时,它还是限制信道容量的一个重要因素。因此,最早人们是企图设计消除或减小通信系统的随机噪声,但是,有时人们也希望获得随机噪声。例如,在实验室中对通信设备或系统进行测试时,有时要故意加入一定的随机噪声,这时则需要产生它。
20世纪40年代末,随着通信理论的发展,仙农(Shannon)就曾指出,在某种情况下,为了实现最有效的通信,应采用具有白噪声的统计特性的信号。另外,为了实现高可靠的保密通信,也希望利用随机噪声。然而,利用随机噪声的最大困难是它难以产生和处理。直到60年代,伪随机噪声的出现才使上述困难得到解决。
伪随机噪声具有类是与随机噪声的一些统计特性,同时又便于重复产生和处理。由于它具有随机噪声的优点,又避免了它的缺点,因此获得了日益广泛的实际应用。目前广泛应用的伪随机噪声都是由数字电路产生的周期序列(即滤波等处理后)得到的。今后我们将这种周期序列称为伪随机序列。
通常产生伪随机序列的电路为一反馈移存器。他又可分为线性反馈移存器和非线性反馈遗存器两类。由线性反馈遗存器产生出的周期最长的二进制数字序列,称为最大长度线性反馈遗存器序列,通常简称为m序列。由于它的理论比较成熟,实现比较简便,实际应用也比较广泛,故这里将重点讨论它。
m序列是最长线性反馈移存器序列的简称,它是由带线性反馈的移存器产生的周期最长的一种序列 。图1就是一个这样的电路。图中示出了n级移位寄存器,其中有若干级经模2加法器反馈到第1级。不难看出,在任何一个时刻去观察移位寄存器的状态,必然是个状态之一,其中每一状态代表一个n位的二进制数字;但是,必须把全0排斥在外,因为如果一个进入全0,不论反馈线多少或在哪些级,这种状态就不会再改变。所以,寄存器的状态可以是非全0的状态之一。这个电路的输出序列是从寄存器移出的,尽管移位寄存器的状态每一移位节拍改变一次,但无疑地是循环的。如果反馈线所分布的级次是恰当的,那么,移位寄存器的状态必然各态历经后才会循环。这里所谓“各态历经”就是所有个状态都经过了。由此可见,应用n级移位寄存器所产生的序列的周期最长是。同时由于这种序列虽然是周期的,但当n足够大时周期可以很长,在一个周期内0和1的排列有很多不同方式,对每一位来说是0还是1,看来好像是随机的,所以又称为伪随机码;又因为它的某一些性质和随机噪声很相似,所以又称为伪噪声码(PN码)。
Gold序列
Gold序列的定义
m序列优选对的两个n次本原多项式乘积构成的新序列为Gold序列,或m序列优选对的两个本原多项式所产生序列的移位模2和新序列也叫做Gold序列[2]。
伪随机序列的应用及其意义
[1]在通信加密中的应用[3]m序列自相关性较好,容易产生和复制,而且具有伪随机性,利用m序列加密数字信号使加密后的信号在携带原始信息的同时具有伪噪声的特点,以达到在信号传输的过程中隐藏信息的目的;在信号接收端,再次利用m序列加以解密,恢复出原始信号。
[2]在雷达信号设计中的应用近年兴起的扩展频谱雷达所采用的信号是已调制的具有类似噪声性质的伪随机序列,它具有很高的距离分辨力和速度分辨力。这种雷达的接收机采用相关解调的方式工作,能够在低信噪比的条件下工作,同时具有很强的抗干扰能力。该型雷达实质上是一种连续波雷达,具有低截获概率性,是一种体制新、性能高、适应现代高技术战争需要的雷达。采用伪随机序列作为发射信号的雷达系统具有许多突出的优点。首先,它是一种连续波雷达,可以较好地利用发射机的功率。其次,它在一定的信噪比时,能够达到很好的测量精度,保证测量的单值性,比单脉冲雷达具有更高的距离分辨力和速度分辨力。最后,它具有较强的抗干扰能力,敌方要干扰这种宽带雷达信号,将比干扰普通的雷达信号困难得多。
[3]在通信系统中的应用伪随机序列是一种貌似随机,实际上是有规律的周期性二进制序列,具有类似噪声序列的性质,在CDMA中,地址码都是从伪随机序列中选取的,在CDMA中使用一种最易实现的伪随机序列:m序列,利用m序列不同相位来区分不同用户;为了数据安全,在CDMA的寻呼信道和正向业务信道中使用了数据掩码(即数据扰乱)技术,其方法是用长度为2的42次方减1的m序列用于对业务信道进行扰码(注意不是扩频),它在分组交织器输出的调制字符上进行,通过交织器输出字符与长码PN码片的二进制模工相加而完成。

-
北京车展:长安汽车引力序列Vision 长安UNI
2025-01-29 07:25:14 查看详情 -
长安汽车高端产品序列概念车定名Vision K正式亮相
2025-01-29 07:25:14 查看详情 -
长安汽车高端产品序列概念车定名Vision 9月28日上市
2025-01-29 07:25:14 查看详情 -
长安马自达CX 长安汽车高端产品序列概念车定名Vision
2025-01-29 07:25:14 查看详情 -
长安汽车高端产品序列概念车定名Vision 售7.77
2025-01-29 07:25:14 查看详情 -
兰博基尼俱乐部 乐高 兰博基尼 序列号 怎么用
2025-01-29 07:25:14 查看详情


 求购
求购



