- kmp算法

kmp算法
基础定义
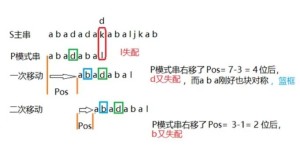 kmp算法(4)字符串的模式匹配是对字符串的基本操作之一,广泛应用于生物信息学、信息检索、拼写检查、语言翻译、数据压缩、网络入侵检测等领域,如何简化其复杂性一直是算法研究中的经典问题。字符串的模式匹配实质上就是寻找模式串P是否在主串T 中,且其出现的位置。我们对字符串匹配的效率的要求越来越高, 应不断地改良模式匹配算法,减少其时间复杂度。
kmp算法(4)字符串的模式匹配是对字符串的基本操作之一,广泛应用于生物信息学、信息检索、拼写检查、语言翻译、数据压缩、网络入侵检测等领域,如何简化其复杂性一直是算法研究中的经典问题。字符串的模式匹配实质上就是寻找模式串P是否在主串T 中,且其出现的位置。我们对字符串匹配的效率的要求越来越高, 应不断地改良模式匹配算法,减少其时间复杂度。
KMP算法是由D.E. Knuth、J.H.Morris和V.R. Pratt提出的,可在一个主文本字符串S内查找一个词W的出现位置。此算法通过运用对这个词在不匹配时本身就包含足够的信息来确定下一个匹配将在哪里开始的发现,从而避免重新检查先前匹配的字符。这个算法是由高德纳和沃恩·普拉特在1974年构思,同年詹姆斯·H·莫里斯也独立地设计出该算法,最终由三人于1977年联合发表。该算法减少了BF算法中i回溯所进行的无谓操作,极大地提高了字符串匹配算法的效率。[1]
字符串的模式匹配
字符串的模式匹配是一种常用的运算。所谓模式匹配,可以简单地理解为在目标(字符串)中寻找一个给定的模式(也是字符串),返回目标和模式匹配的第一个子串的首字符位置。通常目标串比较大,而模式串则比较短小
模式匹配的类型
(1)精确匹配
如果在目标T中至少一处存在模式P,则称匹配成功,否则即使目标与模式只有一个字符不同也不能称为匹配成功,即匹配失败。给定一个字符或符号组成的字符串目标对象T和一个字符串模式P,模式匹配的目的是在目标T中搜索与模式P完全相同的子串,返回T和P匹配的第一个字符串的首字母位置
(2)近似匹配
如果模式P与目标T(或其子串)存在某种程度的相似,则认为匹配成功。常用的衡量字符串相似度的方法是根据一个串转换成另一个串所需的基本操作数目来确定。基本操作由字符串的插入、删除和替换来组成
KMP模式匹配算法
编辑播报
KMP算法是一种改进的字符串匹配算法,其关键是利用匹配失败后的信息,尽量减少模式串与主串的匹配次数以达到快速匹配的目的明 。
求得模式的特征向量之后,基于特征分析的快速模式匹配算法(KMP模式匹配算法)与朴素匹配算法类似,只是在每次匹配过程中发生某次失配时,不再单纯地把模式后移一位,而是根据当前字符的特征数来决定模式右移的位数 。
改进的KMP算法
复旦大学朱洪教授对KMP串匹配算法进行了改进,他主要是修改了next函数,在求 next[j]时,不但要求P[i]=P[j-( next[j]-i)](i=1,2,…, next [j]-1)成立,而且要求P[next[j]]!=p[j]。我们把修改后的next函数计作 Newnext。则计算函数 Newnext值的算法如下 计算函数 Newnext值的算法
计算函数 Newnext值的算法
算法说明
设主串(下文中我们称作T)为:a b a c a a b a c a b a c a b a a b b
模式串(下文中我们称作W)为:a b a c a b
用暴力算法匹配字符串过程中,我们会把T[0] 跟 W[0] 匹配,如果相同则匹配下一个字符,直到出现不相同的情况,此时我们会丢弃前面的匹配信息,然后把T[1] 跟 W[0]匹配,循环进行,直到主串结束,或者出现匹配成功的情况。这种丢弃前面的匹配信息的方法,极大地降低了匹配效率。
而在KMP算法中,对于每一个模式串我们会事先计算出模式串的内部匹配信息,在匹配失败时最大的移动模式串,以减少匹配次数。
比如,在简单的一次匹配失败后,我们会想将模式串尽量的右移和主串进行匹配。右移的距离在KMP算法中是如此计算的:在已经匹配的模式串子串中,找出最长的相同的前缀和后缀,然后移动使它们重叠。
在第一次匹配过程中
T: a b a c aab a c a b a c a b a a b b
W: a b a c ab
在T[5]与W[5]出现了不匹配,而T[0]~T[4]是匹配的,其中T[0]~T[4]就是上文中说的已经匹配的模式串子串,移动找出最长的相同的前缀和后缀并使他们重叠:
T: a b a c aab a c a b a c a b a a b b
W: aba c a b
然后在从上次匹配失败的地方进行匹配,这样就减少了匹配次数,增加了效率。
然而,如果每次都要计算最长的相同的前缀反而会浪费时间,所以对于模式串来说,我们会提前计算出每个匹配失败的位置应该移动的距离,花费的时间就成了常数时间。比如:
| j | 0 | 1 | 2 | 3 | 4 | 5 |
| W[j] | a | b | a | c | a | b |
| F(j) | 0 | 0 | 1 | 0 | 1 | 2 |
当W[j]与T[j]不匹配的时候,设置j = F(j-1).
朱洪对KMP算法作了修改,他修改了KMP算法中的next函数,即求next函数时不但要求W[1,next(j)-1]=W[j-(next(j)-1),j-1],而且要求W[next(j)]<>W[j],他记修改后的next函数为newnext。显然在模式串字符重复高的情况下,朱洪的KMP算法比KMP算法更加有效。
假设在执行正文中自位置 i 起“返前”的一段与模式的自右至左的匹配检查中,一旦发现不匹配(不管在什么位置),则去执行由W[m]与t[i]+d(x)起始的自右至左的匹配检查,这里x是字符t。它的效果相当于把模式向右滑过d(ti)一段距离。显然,若ti不在模式中出现或仅仅在模式末端出现,则模式向右滑过的最大的一段距离m。图1.1示出了执行BM算法时的各种情况。实线连接发现不匹配以后要进行比较的正文和模式中的字母,虚线连接BM算法在模式向右滑后正文和模式中应对齐的字母,星号表示正文中的一个字母。
BM算法由算法1.3给出,函数d的算法由算法1.4给出。计算函数d的时耗显然是Θ(m)。BM算法的最坏情况时耗是Θ(mn)。但由于在实用中这种情况极少出现,因此BM算法仍广泛使用。以下是伪代码:
#include#includeInt KMP(cstring W, cstring T)
{ int i=1, j=1;
while(i<=n){
while (j!=0&&W[j]!=T[i]) j=next[j];
if (j==m) return i-m+1;
else{j++; i++;}
}
return -1;
}
procedureKMP
begin
j=1
j=1
while i<=n do
while j<>0 and W[j]<>T[i] do
j=newnext[j]
endwhile
if j==m
return “success”
else
j++
i++
endif
endwhile
returen “failure”
end
void getNext(string W){
for(int i=1; i0){
j=next[j];
if(W[j]==W[i]{
next[i+1]=j+1;
break;
}
}
}
}
Function NEXT
begin
next[1]=newnext[1]=0
j=2
while j<=m do
i=next[j-1]
while (i<>0 and W[i]<>W[j-1]) do
i=next[i]
endwhile
next[j]=i+1
j=j+1
endwhile
end
function NEWNEXT
begin
newnext[1]=0
j=2
while j<=m do
i=next(j)
if i=0 or W[j]<>W[i+1]
newnext[j]=i
else
newnext[j]=newnext[i]
endif
j++
endwhile
end优化
| j | 0 | 1 | 2 | 3 | 4 | 5 |
| W[j] | a | b | a | c | a | b |
| F(j) | 0 | 0 | 1 | 0 | 1 | 2 |
代码
KMP算法是可以被进一步优化的。
我们以一个例子来说明。譬如我们给的P字符串是“abcdaabcab”,经过KMP算法,应当得到“特征向量”如下表所示:
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(i) | a | b | c | d | a | a | b | c | a | b |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |
但是,如果此时发现p(i) == p(k),那么应当将相应的next[i]的值更改为next[k]的值。经过优化后可以得到下面的表格:
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(i) | a | b | c | d | a | a | b | c | a | b |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |
| 优化的next[i] | -1 | 0 | 0 | 0 | -1 | 1 | 0 | 0 | 3 | 0 |
(1)next[0]= -1 意义:任何串的第一个字符的模式值规定为-1。
(2)next[j]= -1 意义:模式串T中下标为j的字符,如果与首字符相同,且j的前面的1—k个字符与开头的1—k个字符不等(或者相等但T[k]==T[j])(1≤k<j),如:T=”abCabCad” 则 next[6]=-1,因T[3]=T[6].
(3)next[j]=k 意义:模式串T中下标为j的字符,如果j的前面k个字符与开头的k个字符相等,且T[j] != T[k] (1≤k<j)即T[0]T[1]T[2]......T[k-1]==T[j-k]T[j-k+1]T[j-k+2]…T[j-1]且T[j] != T[k].(1≤k<j);
(4) next[j]=0 意义:除(1)(2)(3)的其他情况。
词条图册
| 下标i | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| p(i) | a | b | c | d | a | a | b | c | a | b |
| next[i] | -1 | 0 | 0 | 0 | 0 | 1 | 1 | 2 | 3 | 1 |

-
截断二进制指数退避算法
2025-10-31 17:35:13 查看详情


 求购
求购


