三相

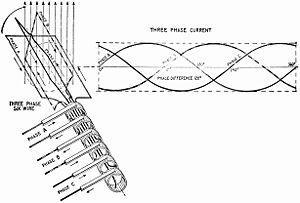一台三相六线制发电机的原理图，每一相（电感）上分别连接着一对传输线

假设有一台使用星型接法的发电机，将其三个负载的加入点命名为L1、L2、L3,则加在三相上的电压分别为：

其中：

代表最大电压,

代表相位角

代表时间，单位为秒

代表频率，单位为转/秒

、和则分别代表L1到中性点（N）、L2到中性点和L3到中性点的电压。

线电压（Line to Line Voltage, Line Voltage）为两条相线间的电压。相电压（V_ph）为负载端所获得的电压，随连接方式而异。

线电流（I_L）为相线上的电流大小。相电流（I_ph）为负载端的电流大小。

星形接法

在星形接法，线电压是相电压的√3倍，线电流等于相电流。

三角形接法

在三角形接法，线电压等于相电压，线电流是相电流的√3倍。

星形接法和三角形接法的总功率，都可使用同一公式计算：

使用相同的阻抗组成电路，三角形接法的功率是星形接法的三倍。

开三角形接法

三角形接法其中一个绕阻被移除，则变成开三角形（Open Delta）。

假设单相变压器可以输出电压V及电流I，两个变压器的功率为

用作三相变压器时，功率为

换言之，两个变压器可使用的功率为原来的86.6%。

对比三个变㱘器，整个系统的功率变成原来的57.7%。因为两个变压器的功率因素不同，其中一个提供无功功率，另一个消耗无功功率，所以可用输出并不是66.7%。

三相变压器，每一相均缠绕着独立的电感

一般在三相的电力系统中，每一相负载的做功的大小均相同。通常会先论证电动机在稳定输出的情况下运作，再考虑不稳定的情况。

三相发电机的特性在于，当各相的负载具有电阻性质时，其输出功率是恒定的。

为了使计算更方便，先定义一个无量纲的功率值作为中间量，则：

代回：

最终结果中不含（相位角）由此可见发电机动率的输出不会随着时间的变化而变化。对于大型发电机来说，这点尤为重要。

实际上，发电机的负载不一定要带有电阻的性质，只需各个相位相等即可，设：

因此最大电流为：

所有相位上的瞬时电流大小为：

这时各个相位的功率输出为：

利用三角恒等式里的积化和差与和差化积公式：

得出瞬时功率输出为：

中括号中的三项互相抵消，得出最终的结果为：

或者

当一个星形接法是平衡负载，即使接上中线也没有电流。流过中性点的电流即三相电流的向量之和，参见基尔霍夫定律。

定义一个非无量纲量的电流，大小为:

流过中线的电流大小为零。因此将中线拿掉而不影响电路本身，证明输出的功率是恒定的。一般三相三线制只有在三相的电源或者负荷都连接在同一个电路上（例如三相电动机），否则各相的输入电压的波动会造成输出功率的不稳定。

在实际的应用中，很少出现理论上输出功率很稳定的情况。利用对称分量法来简化电路，一个不恒定输出的系统可以看作是三个电压分别为正、零、负的恒定输出系统的叠加。

在一个限定的三相电路中，只需要知道三相的模量和流过中性点电流的大小。中性点电流的计算一般先求三相电流的复数之和，在代换回极坐标系的形式。假设三相内的电流分别为, 和，则流经中性点的电流大小为：

最后的极坐标系中的三相和的模量：

在线性的情况下，只有在三相的电源或者负载不均衡的情况下，中性点的电流才不等于零。但是当在实际的使用中，接入的用电器中会使用饱和电抗，光敏、压敏电阻等非线性的电路元件，由于用电器本身电抗的变化，也会造成输出功率的不平衡。

任何一个多相的电路，根据电流随着时间的变化，通过旋转即可生成磁场，这也是异步电动机的工作原理。感应电动机是异步电动机的一种，指的是仅有一套绕组联接电源的异步电动机。

定子三相对称绕组流过三相对称电流时，产生合成基波旋转磁动势。将该磁动势用空间矢量F₀表示，其幅值为

式中，N₁和k_dp1分别为定子绕组的每相串联匝数和基波绕组因数；p为极对数；m₁为定子绕组相数，对于三相异步电动机，m₁=3。

任意两个随着时间t变化的电压之间一定存在着相互位移的关系，同样，一个三相的电源通过变压器可以转化为多相。例如，利用特殊的变压器，能将三相的电源转变为一个二相电源。此类变压器一般称为相位转换器。当三相的电力通过高压线传输到用户的社区在传输到每一户家中时，一般利用角接电容或星接电容将三相变为单项，为家庭用户提供电力。但是相应的，输出功率会有所下降。

用传感器可以测量三相电路的输出功率，无中线要用到两个传感器，有中性线要用到三个。需要使用传感器的数量总是比测量的电路的数量少一个。若采用高压计量，则需要两个电压互感器及两个电流互感器(2VT+2CT)分别用来量度电压及电流。

若使用功率分析仪用来分析谐波电流，宜使用四个电流互感器测量所有带电导体的电流，以提高准确度。