- 机构自由度

机构自由度
正文
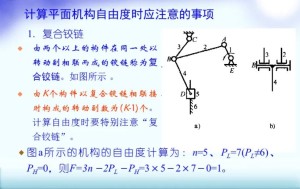 机构自由度(3)使机构具有确定运动时所必须给定的独立运动数目。平面铰链四杆机构,当构件2按给定的角位移规律θ2=θ2(t)运动时,其余各构件的运动就随之确定,因而该机构的自由度数为1。构件2是机构中接受外界独立运动的构件,称为机构的主动件,其余构件称为从动件。欲使机构具有确定运动,应使机构的主动件数等于其自由度数。若机构的主动件数少于机构自由度数,平面铰链五杆机构,只给定主动件 2一个独立运动参数,即构件的角位移规律θ2=θ2(t)时,则其余构件3、4、5的运动并不能确定。若机构的主动件数多于自由度数,则可能使其中驱动功率较小的主动件被迫变为从动件,或使机构卡住不动,甚至遭到破坏。但是,对于平面铰链五杆机构,再给定构件5的角位移规律θ5=θ5(t)时,即同时给定两个独立的运动参数,则此五杆机构的运动完全确定。 一般机构的自由度可凭经验根据几何位置关系直接决定,但常需要通过计算进行验证或作进一步分析。平面机构自由度数的计算公式为
机构自由度(3)使机构具有确定运动时所必须给定的独立运动数目。平面铰链四杆机构,当构件2按给定的角位移规律θ2=θ2(t)运动时,其余各构件的运动就随之确定,因而该机构的自由度数为1。构件2是机构中接受外界独立运动的构件,称为机构的主动件,其余构件称为从动件。欲使机构具有确定运动,应使机构的主动件数等于其自由度数。若机构的主动件数少于机构自由度数,平面铰链五杆机构,只给定主动件 2一个独立运动参数,即构件的角位移规律θ2=θ2(t)时,则其余构件3、4、5的运动并不能确定。若机构的主动件数多于自由度数,则可能使其中驱动功率较小的主动件被迫变为从动件,或使机构卡住不动,甚至遭到破坏。但是,对于平面铰链五杆机构,再给定构件5的角位移规律θ5=θ5(t)时,即同时给定两个独立的运动参数,则此五杆机构的运动完全确定。 一般机构的自由度可凭经验根据几何位置关系直接决定,但常需要通过计算进行验证或作进一步分析。平面机构自由度数的计算公式为
F=3n-2P1-Ph (1)
式中n为一个平面机构中活动构件数(机架作为参考坐标系不计算在内),每个活动构件有3个自由度,即沿X、Y轴的独立移动和绕Z轴的独立转动θz;P1为低副数,每个低副引进2个约束,即限制2个自由度,其中转动副限制x、y两个移动,移动副限制1个转动和另1个移动;Ph为高副数,每个高副只引进1个约束,即限制1个自由度。
应用平面机构自由度的计算公式时需要注意复合铰链,局部自由度和虚约束等几种情况。当几个转动副的轴线重合时称为复合铰链,在计算转动副数时不能遗漏。凸轮机构中从动件如带有滚子,滚子的自转运动即为局部自由度,在计算机构的自由度时应将局部自由度除去不计。机构中引进局部自由度的主要目的是为了减小磨损。虚约束是不起约束作用的约束,当一根轴用两个轴承而形成两个轴线并行的转动副时,其中一个即为虚约束。机构中引进虚约束仅仅是为了提高零件的刚度或渡过机构的死点,但对制造和安装的要求有所提高;否则虚约束就成为实约束,从而使机构产生卡住现象。
计算空间机构的自由度时, 所用的公式类似式 (1),但每个活动构件有 6个自由度;x、y、z、θx、θy和θz。空间运动副可按其相对约束数分为5类,例如球面副有3个相对约束,即x、y、z,称为Ⅲ类运动副;转动副有5 个相对约束,即x、y、z、θx、θy,称为Ⅴ类运动副;其余类推。机构中每个构件受到的或每个运动副具有的相同的约束称为公共约束,铰链四杆机构中,其所有构件只能在X、Y平面内运动,这就使这一平面机构的所有构件的运动受到相同的公共约束,即均不能沿Z轴移动和绕X及Y轴转动,亦即该机构的所有构件共同受到3个公共约束。以表示机构的公共约束数,则机构中每个活动构件的自由度数和每个运动副的有效约束都要减少个。这样,空间机构自由度的计算公式为
(2)
式中Pk为有k个约束的k级运动副数。对于公共约束数m=0的空间机构,其自由度公式为
F=6n-5P5-4P4-3P3-2P2-P1 (3)
平面机构以受到Z、θx和θy三个公共约束,m=3,所以
F=3n-2P5-P4 (4)
式中P5和P4相应为式(1)中的P1和Ph。
m的概念是在1936年由苏联学者提出来的;关于m的具体求法是1952年中国学者最先提出来的"脱离机架法"。这个公式仅适用于求单环机构的自由度。对于多环机构的自由度,中国学者在1979年提出一种比较简单的方法,即先将各环分别按单环计算,最后综合考虑。

-
呼和浩特自由光优惠达2.5万 大气优雅
2025-09-22 02:58:26 查看详情 -
南昌Jeep自由侠优惠8000元 腰线完美
2025-09-22 02:58:26 查看详情 -
呼和浩特自由光优惠达2.5万 成都沃尔沃XC90优惠三万元
2025-09-22 02:58:26 查看详情 -
新款Jeep自由光正式上市 15万元
2025-09-22 02:58:26 查看详情 -
成都别克英朗现金优惠5千元 南昌Jeep自由侠优惠8000元
2025-09-22 02:58:26 查看详情 -
慧灵智障人士社区服务机构
2025-09-22 02:58:26 查看详情 -
北京因私出入境中介机构协会
2025-09-22 02:58:26 查看详情


 求购
求购



