轮子悖论

有两个轮子，其中一个轮子在另一个轮子中间，它们有着不同的直径。它们底边上某点所走过的路径都是直线，乍一看，这两条直线似乎等于两轮的周长。

但是这两条直线有着相同的长度，因此两个轮子的周长必定相同，这与两个轮子有着不同的直径是相互矛盾的，这就是所谓的轮子悖论。

这个悖论存在的漏洞就在于，假定小一点的轮子的进行轨迹为其周长。事实上，对两个轮子来说，想要做出完全相同的运动是不可能的。小一点的轮子并没有如图1所示从点3转动到点4，而是被大轮子拽着沿着这条直线前进。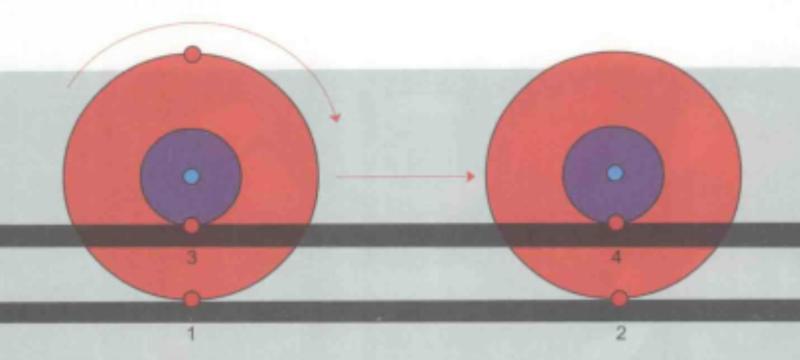图1：轮子悖论

从物理学角度来看，如果两个半径不同的同心轮子沿着一条平行线转动，那么其中至少会有一个打滑。如果利用齿轮系统防止打滑，那么轮子就会出现被卡住的情况。

在当代类似的实验中，这种情况通常会在司机将车停在路边时无意中发生。实验发现，尽管轮毂不断转动并发出刺耳声音，但汽车外胎并没有出现打滑的情况。

从数学角度来看，内圆的点的数量与外圆的点的数量是完全一样的，即这两个圆之间存在着一种双射的情况（一种对应关系）。这并不能运用到轮子实体上，因为他们是由离散的原子组成的。因此在车轮的密度、宽度与厚度等都相同的情况下（不同的只是他们之间的半径），较大车轮的原子数量肯定要更多一些。^[1]