- 离差

离差
反映离散程度
基本介绍
离差即标志变动度,又称“偏差”,是观测值或估计量的平均值与真实值之间的差,是反映数据分布离散程度的量度之一,或说是反映统计总体中各单位标志值差别大小的程度或离差情况的指标,常写作![]() ,即参与计算平均数的变量值与平均数之差。离差的性质有二: (1)离差的代数和等于0;(2)参与计算平均数的各变量值与平均数之差的平均和,小于这些变量值与平均数之外的任何数之差的平均和。由于这两种性质,使离差在描述统计中运用较广。
,即参与计算平均数的变量值与平均数之差。离差的性质有二: (1)离差的代数和等于0;(2)参与计算平均数的各变量值与平均数之差的平均和,小于这些变量值与平均数之外的任何数之差的平均和。由于这两种性质,使离差在描述统计中运用较广。
在统计中用来测定标志变动度的指标主要有:平均差、标准差。全距,四分位差,十分位差和离散系数等,离差是测定样本代表性的重要指标,例如我们在选择时,有两组工人,每组都是5人,第一组每人日产分别为10,23,45,52,60,平均每人日产38件;第二组每人日产分别为35,39,42,39,38,平均每人日产也是38件,但我们可以看出,第二组的样本较第一组样本更加接近平均数,因此,第二组代表也较第一组强,从这里可以看出,标志变动度越小,样本的代表性较强,反之,则样本的代表性越强。
尽管集中量可以很好地描述一组数据的特征,但仅用这些统计量还是不够的。还需要考虑数据的分散情况。有时,两组数据的平均数和中位数可能完全相同,但这两组数据之间会存在着很大的区别。请看下面两组数据:
A组:79 79 79 80 81 81 81
B组:50 60 70 80 90 100 100
这两组数据的平均数和中位数均为80,但不能据此就简单认为这两组学生的水平是一样的。A组数据与B组数据之间显然是有区别的。首先,A组中的数据相对比较集中,每个数据的值与平均数80相差无几;而B组中的数据相对分散一些,参差不齐,它反映了数据分布的另一个重要特征——变异性(variability)。描述数据离散趋势的统计量称为离散量(measures of dispersion),或称差异量。
集中量描述了一组数据的典型情况,离散量则反映了数据的特殊情况。在研究一组数据的特征时,不但要了解其典型情况,而且还要了解其特殊情况,前面的例子中A组数据和B组数据的集中量相同,但其离散量肯定是不同的,只有同时了解了这两组数据的集中量和离散量,才能更为透彻地了解这两组数据之间的差别。常用的表示数据离散趋势的统计指标有全距、四分位区间距、平均差、方差和标准差。
全距
全距是说明数据离散程度的最简单的统计量。把一组数据按从小到大的顺序排列,用最高分减去最低分,所得的值就是全距,即最高分和最低分之问的距离。上面A组数据的全距为81-79=2;B组数据的全距为100-50=50。全距小,说明数据的分布相对集中;全距大,说明数据的分布较为分散。全距的优点是计算方法简单,而且也容易理解。缺点是由于它只考虑到两端的数值,没有考虑中间数值的差异情况,描述数据时不太稳定。
四分位区间距
中位数可以用来表示一组数据分布的集中趋势。中位数正好把一组数据一分为二。如果把中位数左侧和右侧的分布再各分成两个部分,得到的是四个相等的分位。这组数据的第一个四分位(即25%的位置)的值正好处于数据分布的四分之一处,中位数正好是第二个四分位的值,第三个四分位的值刚好位于该组数据分布的四分之三处。把第三个四分位的值减去第一个四分位的值,所得到的值叫做四分位区间距(inter-quartile range,IQR),统计学上也用这种方法来表示数据的离散情况。如上面A组数据的四分位区间距为81-79=2;B组数据的四分位区间距为100-60=40。除了四分位区间距,统计学上还有十分位区间距和百分位区间距,它们的区分方法相同,十分位则将数据由大到小或由小到大排序后,用9个点将全部数据分为十等份,与9个点位置上相对应的变量称为十分位数(deciles),分别记为D1,D2,...,D9,表示10%的数据落在D1下,20%的数据落在D2下……100%的数据落在D9下。百分位区间距与十分位区间距同例,只是将数据分成100等份,于99个分割点位置上相对应的变量称为百分位数(Percentiles),分别记为P1,P2,…,P99,表示1%的数据落在P1下……99%的数据落在P99下。
平均差
与全距相比,四分位区间距在表述数据的离散情况时稍微好一些,但由于它没有把所有的数据都考虑在内,其稳定性会差一些。比如说,我们得到两组数据,这两组数据的值并不完全一样,但最后得到的四分位区间距的值则可能完全一致,这便是用四分位区问距来表示数据分布的不足之处。理想的办法是把全部数据都考虑在内来计算分布程度。理由很简单:平均数代表一组数据的集中趋势,我们把一组数据中的每个数据与平均数相比较就可以得知每个数据与平均数偏离的程度,或者说与平均数差异的情况。如果把这组数据中每个数据与平均数差异的情况相加起来,那么所有数据的差异情况便一目了然。把这个值除以数据的个数,所得的值叫做平均差。其计算公式为:
平均差=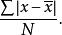
其中,![]() =每个数据的值;
=每个数据的值;
![]() =总体平均数;
=总体平均数;
N=观测的数据个数。
从上式可知,平均差是数据分布中所有原始数据与平均数距离的绝对值的平均。用绝对值是为了不出现负数。由于平均差是根据分布中每一个观测值计算求得的,它较好地代表了数据分布的离散程度。然而,由于平均差的计算要求绝对值,不利于进一步的统计分析,故在统计实践中平均差不常使用。
方差与标准差
根据上面的公式,如果不求每个原始数据与平均数之差的绝对平均值,而是求它们之间的平方,这样就不会有负数出现了。然后再把每个原始数据与平均数之差的平方的值加起来,得到的是每个原始数据与平均数之差的平方和: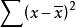 。用这个平方和再除以所观测到的数据的个数,得到的值被称作方差。用公式表示为:
。用这个平方和再除以所观测到的数据的个数,得到的值被称作方差。用公式表示为: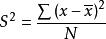 。由于方差的值相对来说比较大,一般情况下人们使用标准差来代表数据的离散程度。标准差就是方差的平方根,其计算公式为:
。由于方差的值相对来说比较大,一般情况下人们使用标准差来代表数据的离散程度。标准差就是方差的平方根,其计算公式为: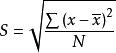 。标准差与方差的概念易于理解,它们实际上都是一个差异量数:标准差的平方就是方差,或方差的平方根就等于标准差,二者都反映了一组数据围绕平均数分布的情况。标准差的值越大,表明这组数据的离散程度也越大,即数据越参差不齐,分布范围越广;标准差的值越小,表明这组数据的离散程度越小,即数据越集中、整齐,分布范围越小。当数据完全没有差异时,所有数值都与平均数相等,这时标准差或方差等于零。
。标准差与方差的概念易于理解,它们实际上都是一个差异量数:标准差的平方就是方差,或方差的平方根就等于标准差,二者都反映了一组数据围绕平均数分布的情况。标准差的值越大,表明这组数据的离散程度也越大,即数据越参差不齐,分布范围越广;标准差的值越小,表明这组数据的离散程度越小,即数据越集中、整齐,分布范围越小。当数据完全没有差异时,所有数值都与平均数相等,这时标准差或方差等于零。
有一点需要说明:在上述公式中我们用N作为除数,所得结果并不是十分准确的。这是因为在一般情况下,总体参数是未知的,只能用样本统计量作估计值,譬如用样本标准差(S)作为总体标准差(![]() )的估计值。可以证明,在公式中用N作为除数时(尤其是当N很小时),所得出的作为总体标准差估计值的样本标准差是有偏差的,而N-1作除数时,所得标准差则是无偏差的。因此,比较稳妥的做法是用N-1作除数。当然,当N比较大时,用N或N-1作除数,所得结果差别不大[2]。
)的估计值。可以证明,在公式中用N作为除数时(尤其是当N很小时),所得出的作为总体标准差估计值的样本标准差是有偏差的,而N-1作除数时,所得标准差则是无偏差的。因此,比较稳妥的做法是用N-1作除数。当然,当N比较大时,用N或N-1作除数,所得结果差别不大[2]。
点于直线离差
直角坐标平面上,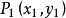 点到直线
点到直线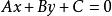 的距离
的距离
![]() 若直线方程用法线式,则
若直线方程用法线式,则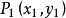 点到直线
点到直线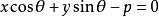 的距离
的距离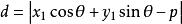 。
。
根据这一公式,求一点到一条直线的距离,只要先把这条直线的方程化成法线式,然后把已知点的坐标代入方程的左边,计算所得值的绝对值,就是所求的距离。
若将公式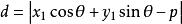 ,写成
,写成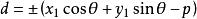 ,则其中的正负号应这样确定:①当已知点和原点在直线的两侧时取正号;②当已知点和原点在直线的同侧时取负号;③若直线过原点但不与Y轴重合,则已知点在直线上方时取正号,在直线下方时取负号;④若直线与Y轴重合,则已知点在直线右方时取正号,在直线左方时取负号。
,则其中的正负号应这样确定:①当已知点和原点在直线的两侧时取正号;②当已知点和原点在直线的同侧时取负号;③若直线过原点但不与Y轴重合,则已知点在直线上方时取正号,在直线下方时取负号;④若直线与Y轴重合,则已知点在直线右方时取正号,在直线左方时取负号。
![]() 或
或
![]()
![]() 叫做直线
叫做直线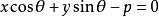 或
或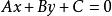 关于点
关于点![]() 的离差。
的离差。
离差δ的正负的判定法则是:①当![]() ,或
,或![]() 时,若点
时,若点![]() 与原点在直线的同侧,则
与原点在直线的同侧,则![]() ;异侧,则
;异侧,则![]() ;②当
;②当![]() ,或
,或![]() (直线过原点)时,若点
(直线过原点)时,若点![]() 与点
与点![]() 在直线同侧,则
在直线同侧,则![]() ;异侧,则
;异侧,则![]() ;③当
;③当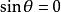 且
且![]() ,或
,或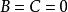 (直线为Y轴)时,若点
(直线为Y轴)时,若点![]() 在直线右侧,则
在直线右侧,则![]() ;左侧,则
;左侧,则![]() 。
。
离差不仅反映出点到直线的距离,而且显示出点相对于直线的方位[3]。



 求购
求购




