- 数学符号

数学符号
基础定义
符号(Symbol) 意义(Meaning)
= 等于 is equal to
≠ 不等于 is not equal to
≈ 约等于 approximately equal to
< 小于 is less than
> 大于 is greater than
// 平行 is parallel to
![]()
平行且相等
⊥ 垂直
≥ 大于或等于 is greater than or equal to
≤ 小于或等于 is less than or equal to
≡ 恒等于或 同余
π 圆周率 约为3.1415926536Ratio of circumference to diameter; Pi
e 自然常数 约为 2.7182818285Natural constant
|x| 绝对值或(复数的) 模absolute value of X
 数学符号
数学符号
∽ 相似 is similar to
≌ 全等 is equal to(especially for geometric figure)
![]()
远大于
<< 远小于
∪ 并集
∩ 交集
⊆ 包含于
∈ 属于
⊙ 圆
\ 除,求商值,部分编程语言中理解为 整除
α, β, γ, φ… 角度; 系数
∞ 无穷大(包括正无穷大+∞与负无穷大-∞)
ln x 以e为底的 对数( 自然对数)
lg x 以10为底的对数( 常用对数)
lbx 以2为底的对数
lim 求极限
floor( x) 或[x],亦可写为
![]()
下取整函数(直译为“地板函数”),又称 高斯函数
ceil( x) 亦可写为
![]()
上取整函数(直译为“天花板函数”)
x mod y模,求 余数
x-floor( x) 或{x} 表示x的小数部分
d y,d f( x) 函数 y=f( x)的微分(或线性主部)
∫ f( x)d x 不定积分,函数 f的全体原函数
平面二维k-ε紊流模型不同壁函数的对比及研究
函数 f从 a到 b的 定积分
表示 i从 m到 n逐一递增对 连加 求和(sigma:∑ )
表示 i从 m到 n逐一递增对 连乘求积 (pi:Π)
演绎过程
例如 加号曾经有好几种,目前通用“+”号。  数学符号“+”号是由拉丁文“et”(“和”的意思)演变而来的。十六世纪,意大利科学家 塔塔里亚用 意大利文“plu”(“加”的意思)的第一个字母表示加,草为“μ”最后都变成了“+”号。“-”号是从拉丁文“minus”(“减”的意思)演变来的,一开始简写为m,再因快速书写而简化为“-”了。
数学符号“+”号是由拉丁文“et”(“和”的意思)演变而来的。十六世纪,意大利科学家 塔塔里亚用 意大利文“plu”(“加”的意思)的第一个字母表示加,草为“μ”最后都变成了“+”号。“-”号是从拉丁文“minus”(“减”的意思)演变来的,一开始简写为m,再因快速书写而简化为“-”了。
也有人说,卖酒的商人用“-”表示酒桶里的酒卖了多少。以后,当把新酒灌入大桶的时候,就在“-”上加一竖,意思是把原线条勾销,这样就成了个“+”号。
到了十五世纪,德国数学家魏德美正式确定:“+”用作加号,“-”用作 减号。
乘号曾经用过十几种,现代数学通用两种。一个是“×”,最早是英国数学家奥屈特1631年提出的;一个是“·”,最早是英国数学家赫锐奥特首创的。德国数学家 莱布尼茨认为:“×”号像拉丁字母“X”,可能引起混淆而加以反对,并赞成用“·”号(事实上点乘在某些情况下亦易与小数点相混淆)。后来他还提出用“∩“表示 相乘。这个符号在现代已应用到 集合论中了。
到了十八世纪,美国数学家欧德莱确定,把 “×”作为乘号。他认为“×”是“+”的旋转变形,是另一种表示增加的符号。
“÷”最初作为减号,在欧洲大陆长期流行。直到1631年英国数学家奥屈特用“:”表示 除或 比,另外有人用“-”(除线)表示除。后来 瑞士数学家 拉哈在他所著的《 代数学》里,才根据群众创造,正式将“÷”作为 除号。
平方根号曾经用拉丁文“Radix”(根)的首尾两个字母合并起来表示,十七世纪初叶,法国数学家 笛卡儿在他的《 几何学》中,第一次用 “√”表示 根号。“√”是由拉丁字线“r”的变形,“ ̄”是括线。
十六世纪法国数学家维叶特用 “=”表示两个量的差别。可是英国 牛津大学数学、修辞学教授列考尔德觉得:用两条平行而又相等的直线来表示两数相等是最合适不过的了,于是等于符号“=”就从1540年开始使用起来。
1591年,法国数学家 韦达在 菱形中大量使用这个符号,才逐渐为人们接受。十七世纪德国 莱布尼茨广泛使用了“=”号,他还在几何学中用 “∽”表示 相似,用 “≌”表示 全等。
大于号 “>”和小于号 “<”,是1631年英国著名 代数学家赫锐奥特创用。至于 “≥”、“≤”、“≠”这三个符号的出现,是很晚很晚的事了。 大括号 “{}”和 中括号 “[]”是代数创始人之一魏治德创造的。
任意号(全称量词)∀来源于英语中的any一词,因为小写和大写均容易造成混淆,故将其单词首字母大写后倒置。同样,存在号(存在量词)∃来源于exist一词中E的反写。
应用举例
数量符号
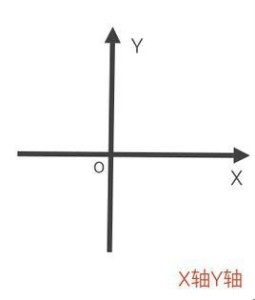 数学符号如:i,
数学符号如:i,
![]()
,a,x,e,π。详见下。
运算符号
如 加号(+), 减号(-), 乘号(×或·), 除号(÷或/),两个 集合的 并集(∪), 交集(∩), 根号(√ ̄), 对数(log,lg,ln,lb), 比(:), 绝对值符号| |, 微分(d),积分(∫),闭合曲面(曲线) 积分(∮)等。
关系符号
如“=”是 等号,“≈”是近似符号(即 约等于),“≠”是 不等号,“>”是 大于符号,“<”是 小于符号,“≥”是大于或等于符号(也可写作“≮”,即不小于),“≤”是小于或等于符号(也可写作“≯”,即不大于),“→ ”表示变量变化的趋势,“∽”是相似符号,“≌”是全等号,“∥”是平行符号,“⊥”是垂直符号,“∝”是 正比例符号(表示 反比例时可以利用 倒数关系),“∈”是属于符号,“⊆”是包含于符号,“⊇”是包含符号,“|”表示“能 整除”(例如 a| b 表示“ a能整除 b”,而
![]()
||b表示r是a恰能整除b的最大幂次), x,y等任何字母都可以代表 未知数。
结合符号
如小 括号“()”, 中括号“[ ]”, 大括号“{ }”,横线“—”,比如
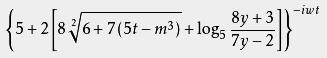
。
性质符号
如 正号“+”, 负号“-”, 正负号“
![]()
”(以及与之对应使用的负正号“
![]()
”)
省略符号
如 三角形(△),直角三角形( Rt△), 正弦( sin)(见 三角函数),
 数学符号
数学符号
双曲正弦函数( sinh), x的 函数( f(x)), 极限( lim), 角(∠),
∵ 因为(一个脚站着的,站不住)
∴ 所以(两个脚站着的,能站住)(口诀:因为站不住,所以两个点;因为上面两个点,所以下面两个点)
总和,连加: ∑,求积,连乘: ∏,从n个元素中取出r个元素所有不同的 组合数
![]()
( n元素的总个数; r参与选择的元素个数), 幂
![]()
等。
排列组合
C 组合数
A (或P) 排列数
n 元素的总个数
r 参与选择的元素个数
! 阶乘,如5!=5×4×3×2×1=120,规定0!=1
!! 半阶乘(又称 双阶乘),例如7!!=7×5×3×1=105,10!!=10×8×6×4×2=3840
离散符号
∀ 全称量词
∃ 存在量词
├ 断定符(公式在 L中可证)
╞ 满足符(公式在 E上有效,公式在 E上可满足)
﹁ 命题的“非”运算,如 命题的否定为﹁ p
∧ 命题的“ 合取”(“ 与”)运算
∨ 命题的“ 析取”(“ 或”,“可兼或”)运算
→ 命题的“条件”运算
↔ 命题的“双条件”运算的
p<=> q 命题 p与 q的 等价关系
p=> q 命题 p与 q的 蕴涵关系(p是q的 充分条件,q是p的 必要条件)
A* 公式 A的对偶公式,或表示A的 数论倒数(此时亦可写为
![]()
)
wff 合式公式
iff 当且仅当
↑ 命题的“ 与非” 运算( “ 与非门” )
↓ 命题的“ 或非”运算( “ 或非门” )
□ 模态词“必然”
◇ 模态词“可能”
∅ 空集
∈ 属于(如" A∈ B",即“ A属于 B”)
∉ 不属于
P( A) 集合 A的 幂集
| A| 集合 A的点数
R²=R○R [R =R ○R] 关系R的“复合”
ℵ Aleph,阿列夫
⊆ 包含
⊂(或⫋) 真包含
另外,还有相应的⊄,⊈,⊉等
∪ 集合的并运算
U(P)表示P的领域
∩ 集合的交运算
-或\ 集合的差运算
〡 限制
集合关于关系 R的 等价类
A/ R 集合 A上关于 R的 商集
[ a] 元素 a产生的 循环群
I环,理想
Z/( n) 模 n的 同余类集合
r( R) 关系 R的自反 闭包
s( R) 关系 R的对称闭包
CP 命题演绎的定理(CP 规则)
EG 存在推广规则( 存在量词引入规则)
ES 存在量词特指规则(存在量词消去规则)
UG 全称推广规则( 全称量词引入规则)
US 全称特指规则(全称量词消去规则)
R 关系
r 相容关系
R○S 关系 与关系 的复合
domf 函数 的 定义域(前域)
ranf 函数 的 值域
f: x→ yf是 x到 y的 函数
( x, y) x与 y的 最大公约数,有时为避免混淆,使用 gcd(x,y)
[ x, y] x与 y的 最小公倍数,有时为避免混淆,使用 lcm(x,y)
aH( Ha) H关于 a的左(右) 陪集
Ker( f) 同态映射 f的核(或称 f同态核)
[1, n] 1到 n的 整数集合
d( A, B),| AB|,或 AB 点 A与点 B间的距离
d( V) 点 V的 度数
G=( V, E) 点集为 V,边集为 E的图 G
W( G) 图 G的 连通分支数
k( G) 图 G的点 连通度
Δ( G) 图 G的最大点度
A( G) 图 G的 邻接矩阵
P(G) 图 G的 可达矩阵
M( G) 图 G的 关联矩阵
C 复数集
I 虚数集
N 自然数集,非负整数集(包含元素"0")
N*( N +) 正自然数集,正整数集(其中*表示从集合中去掉元素“0”,如 R*表示非零实数)
P 素数( 质数)集
Q 有理数集
R 实数集
Z 整数集
Set 集范畴
Top 拓扑空间范畴
Ab 交换群范畴
Grp 群范畴
Mon 单元半群范畴
Ring 有单位元的(结合)环范畴
Rng 环范畴
C Rng 交换环范畴
R-mod 环 R的左模范畴
mod- R 环 R的右模范畴
Field 域范畴
Poset 偏序集范畴
希腊字母
序号 |
大写 |
小写 |
英语音标注音 |
英文 |
汉字注音 |
常用指代意义 |
1 |
Α |
α |
/'ælfə/ |
alpha |
阿尔法 |
角度,系数,角加速度,第一个 |
2 |
Β |
β |
/'bi:tə/或/'beɪtə/ |
beta |
贝塔 /毕塔 |
磁通系数,角度,系数 |
3 |
Γ |
γ |
/'gæmə/ |
gamma |
伽玛 /甘玛 |
电导系数,角度,比热容比 |
4 |
Δ |
δ |
/'deltə/ |
delta |
得尔塔 /岱欧塔 |
变化量,化学反应中的加热,屈光度,一元二次方程中的判别式 |
5 |
Ε |
ε |
/'epsɪlɒn/ |
epsilon |
埃普西龙 |
对数之基数,介电常数 |
6 |
Ζ |
ζ |
/'zi:tə/ |
zeta |
泽塔 |
系数,方位角,阻抗,相对黏度 |
7 |
Η |
η |
/'i:tə/ |
eta |
伊塔 /诶塔 |
迟滞系数,效率 |
8 |
Θ |
θ |
/'θi:tə/ |
theta |
西塔 |
温度,角度 |
9 |
Ι |
ι |
/aɪ'əʊtə/ |
iota |
埃欧塔 |
微小,一点 |
10 |
Κ |
κ |
/'kæpə/ |
kappa |
堪帕 |
介质常数,绝热指数 |
11 |
∧ |
λ |
/'læmdə/ |
lambda |
兰姆达 |
波长,体积,导热系数 |
12 |
Μ |
μ |
/mju:/ |
mu |
谬/穆 |
磁导系数,微,动摩擦系(因)数,流体动力黏度,微(千分之一),放大因数(小写) |
13 |
Ν |
ν |
/nju:/ |
nu |
拗/奴 |
磁阻系数,流体运动粘度,光子频率,化学计量数 |
14 |
Ξ |
ξ |
希腊/ksi/ 英美/ˈzaɪ/或/ˈsaɪ/ |
xi |
可西 /赛 |
随机变量,(小)区间内的一个未知特定值 |
15 |
Ο |
ο |
/əuˈmaikrən/ 或/ˈɑmɪˌkrɑn/ |
omicron |
欧(阿~)米可荣 |
高阶无穷小函数 |
16 |
∏ |
π |
/paɪ/ |
pi |
派 |
圆周率=圆周÷直径≈3.1416,π(n)表示不大于n的质数个数 |
17 |
Ρ |
ρ |
/rəʊ/ |
rho |
柔/若 |
电阻系数,柱坐标和极坐标中的极径,密度 |
18 |
∑ |
σ,ς |
/'sɪɡmə/ |
sigma |
西格玛 |
总和,表面密度,跨导,正应力 |
19 |
Τ |
τ |
/tɔ:/或/taʊ/ |
tau |
套/驼 |
时间常数,切应力,2π(两倍圆周率) |
20 |
Υ |
υ |
/ˈipsɪlon/ 或/ˈʌpsɪlɒn/ |
upsilon |
宇(阿~)普西龙 |
位移 |
21 |
Φ |
φ |
/faɪ/ |
phi |
弗爱 /弗忆 |
磁通,辅助角,透镜焦度,热流量 |
22 |
Χ |
χ |
/kaɪ/ |
chi |
凯/柯义 |
统计学中有卡方(χ^2)分布 |
23 |
Ψ |
ψ |
/psaɪ/ |
psi |
赛/普赛/普西 |
角速,介质电通量,ψ函数 |
24 |
Ω |
ω |
/'əʊmɪɡə/ 或/oʊ'meɡə/ |
omega |
欧米伽 /欧枚嘎 |
欧姆,角速度,交流电的电角度,化学中的质量分数 |
主要应用
C Rng 交换环范畴
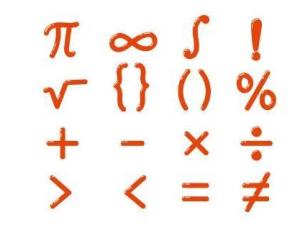 数学符号R-mod 环 R的左模范畴
数学符号R-mod 环 R的左模范畴
Field 域范畴
Poset 偏序集范畴
其他信息
序号 |
大写 |
小写 |
英语音标注音 |
英文 |
汉字注音 |
常用指代意义 |
1 |
Α |
α |
/'ælfə/ |
alpha |
阿尔法 |
角度,系数,角加速度,第一个 |
2 |
Β |
β |
/'bi:tə/或/'beɪtə/ |
beta |
贝塔 /毕塔 |
磁通系数,角度,系数 |
3 |
Γ |
γ |
/'gæmə/ |
gamma |
伽玛 /甘玛 |
电导系数,角度,比热容比 |
4 |
Δ |
δ |
/'deltə/ |
delta |
得尔塔 /岱欧塔 |
变化量,化学反应中的加热,屈光度,一元二次方程中的判别式 |
5 |
Ε |
ε |
/'epsɪlɒn/ |
epsilon |
埃普西龙 |
对数之基数,介电常数 |
6 |
Ζ |
ζ |
/'zi:tə/ |
zeta |
泽塔 |
系数,方位角,阻抗,相对黏度 |
7 |
Η |
η |
/'i:tə/ |
eta |
伊塔 /诶塔 |
迟滞系数,效率 |
8 |
Θ |
θ |
/'θi:tə/ |
theta |
西塔 |
温度,角度 |
9 |
Ι |
ι |
/aɪ'əʊtə/ |
iota |
埃欧塔 |
微小,一点 |
10 |
Κ |
κ |
/'kæpə/ |
kappa |
堪帕 |
介质常数,绝热指数 |
11 |
∧ |
λ |
/'læmdə/ |
lambda |
兰姆达 |
波长,体积,导热系数 |
12 |
Μ |
μ |
/mju:/ |
mu |
谬/穆 |
磁导系数,微,动摩擦系(因)数,流体动力黏度,微(千分之一),放大因数(小写) |
13 |
Ν |
ν |
/nju:/ |
nu |
拗/奴 |
磁阻系数,流体运动粘度,光子频率,化学计量数 |
14 |
Ξ |
ξ |
希腊/ksi/ 英美/ˈzaɪ/或/ˈsaɪ/ |
xi |
可西 /赛 |
随机变量,(小)区间内的一个未知特定值 |
15 |
Ο |
ο |
/əuˈmaikrən/ 或/ˈɑmɪˌkrɑn/ |
omicron |
欧(阿~)米可荣 |
高阶无穷小函数 |
16 |
∏ |
π |
/paɪ/ |
pi |
派 |
圆周率=圆周÷直径≈3.1416,π(n)表示不大于n的质数个数 |
17 |
Ρ |
ρ |
/rəʊ/ |
rho |
柔/若 |
电阻系数,柱坐标和极坐标中的极径,密度 |
18 |
∑ |
σ,ς |
/'sɪɡmə/ |
sigma |
西格玛 |
总和,表面密度,跨导,正应力 |
19 |
Τ |
τ |
/tɔ:/或/taʊ/ |
tau |
套/驼 |
时间常数,切应力,2π(两倍圆周率) |
20 |
Υ |
υ |
/ˈipsɪlon/ 或/ˈʌpsɪlɒn/ |
upsilon |
宇(阿~)普西龙 |
位移 |
21 |
Φ |
φ |
/faɪ/ |
phi |
弗爱 /弗忆 |
磁通,辅助角,透镜焦度,热流量 |
22 |
Χ |
χ |
/kaɪ/ |
chi |
凯/柯义 |
统计学中有卡方(χ^2)分布 |
23 |
Ψ |
ψ |
/psaɪ/ |
psi |
赛/普赛/普西 |
角速,介质电通量,ψ函数 |
24 |
Ω |
ω |
/'əʊmɪɡə/ 或/oʊ'meɡə/ |
omega |
欧米伽 /欧枚嘎 |
欧姆,角速度,交流电的电角度,化学中的质量分数 |
词条图册
 数学符号 在 Microsoft Word中可以插入一般应用条件下的所有数学符号,以Word2010软件为例介绍操作方法:第1步,打开Word2010文档窗口,单击需要添加数学符号的公式,并将插入条光标定位到目标位置。第2步,在“公式工具/设计”功能区的“符号”分组中,单击“其他”按钮打开符号面板。默认显示的“基础数学”符号面板。用户可以在“基础数学”符号面板中找到最常用的数学符号。同样地,Alt+41420(即压下Alt不放,依次按41420(小键盘),最后放开Alt 就可以打出 √。
数学符号 在 Microsoft Word中可以插入一般应用条件下的所有数学符号,以Word2010软件为例介绍操作方法:第1步,打开Word2010文档窗口,单击需要添加数学符号的公式,并将插入条光标定位到目标位置。第2步,在“公式工具/设计”功能区的“符号”分组中,单击“其他”按钮打开符号面板。默认显示的“基础数学”符号面板。用户可以在“基础数学”符号面板中找到最常用的数学符号。同样地,Alt+41420(即压下Alt不放,依次按41420(小键盘),最后放开Alt 就可以打出 √。



 求购
求购








