- 平移

平移
基础定义
在仿射几何,平移(translation)是将物件的每点向同一方向移动相同距离。[1]
它是等距同构,是仿射空间中仿射变换的一种。它可以视为将同一个向量加到每点上,或将坐标系统的中心移动所得的结果。即是说,若![]() 是一个已知的向量,
是一个已知的向量,![]() 是空间中一点,平移
是空间中一点,平移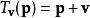 。
。
将同一点平移两次,结果可用一次平移表示,即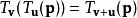 ,因此所有平移的集是一个群,称为平移群。这个群和空间同构,又是欧几里德群E(n)的正规子群。
,因此所有平移的集是一个群,称为平移群。这个群和空间同构,又是欧几里德群E(n)的正规子群。
T对E的商群与正交群O(n)同构:E(n) / T = O(n)。
基本性质
经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行且相等。
平移变换不改变图形的形状、大小和方向(平移前后的两个图形是全等形)。
(1)图形平移前后的形状和大小没有变化,只是位置发生变化。
(2)图形平移后,对应点连成的线段平行(或在同一直线上)且相等。
(3)多次连续平移相当于一次平移。
(4)偶数次对称后的图形等于平移后的图形。
(5)平移是由方向和距离决定的。
(6)经过平移,对应线段平行(或共线)且相等,对应角相等,对应点所连接的线段平行(或共线)且相等。
这种将图形上的所有点都按照某个方向作相同距离的位置移动,叫做图形的平移运动,简称为平移
平移的条件:确定一个平移运动的条件是平移的方向和距离。
三个要点
1 原来的图形的形状和大小和平移后的图形是全等的。
2 平移的方向。(东南西北,上下左右,东偏南n度,东偏北n度,西偏南n度,西偏北n度)
3 平移的距离。(长度,如7厘米,8毫米等)
平移作用
1.通过简单的平移可以构造精美的图形。也就是花边,通常用于装饰,过程就是复制-平移-粘贴。
2.平移常与平行线有关,平移可以将一个角,一条线段,一个图形平移到另一个位置,是分散的条件集中到一个图形上,使问题得到解决。
总体归纳
1 把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同。
2 新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点。连接各组对应点的线段平行且相等(或在同一直线上)。
平移特征
1 平移前后图形的形状、大小不变,只是位置发生改变。
2 新图形与原图形的对应点所连的线段平行且相等(或在同一直线上)。
3 新图形与原图形的对应线段平行且相等,对应角相等。[2]
画法
以画雪人为例。可以把半透明纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个……而求必须水平或垂直于原图。根据平移的方向,作出每一个图形要点的平移点(如:直线的顶点,圆的圆心等)
方法是通过原来图形的点作平移方向的平行线,并取距离为平移的长度的点 用三角板的话,第一块三角板斜边对齐平移方向;第二块三角板斜边贴住第一块三角板的直角边作为第一块三角板移动的准线(之后第二块三角板必须保持固定);第一块三角板沿着第二块三角板斜边移动到相应的点,轻轻画出平行线(以后要擦除),在平行线上量出平移的距离的点就是目标“平移点”;2,根据平移点,作出原来的图形(如:直线只要直接连接两个端点,以平移圆心为圆心作等半径的圆。
(1)找出原图形的关键点(如顶点或者端点);
(2)按要求分别描出各个关键点平移后的对应点;
(3)按原图将各对应点顺次连接。
矩阵表示
例如在三维空间,使用齐次坐标,![]() 可用矩阵表示为
可用矩阵表示为
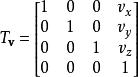
平移的结果![]() 就是
就是
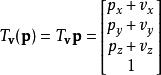
平移的逆矩阵: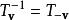 。两个平移矩阵的积就是两次平移的结果:
。两个平移矩阵的积就是两次平移的结果: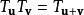 。因为向量加法符合交换律,所以平移群不像一般矩阵乘法,平移矩阵乘法是可交换的。[2]
。因为向量加法符合交换律,所以平移群不像一般矩阵乘法,平移矩阵乘法是可交换的。[2]



 求购
求购




