- 拐点

拐点
中文名
拐点
适用范围
数理科学
又名
反曲点
定义
设函数y=f(x)在点![]() 的某邻域内连续,若(
的某邻域内连续,若(![]() ,f(
,f(![]() ))是曲线y=f(x)凹与凸的分界点,则称(
))是曲线y=f(x)凹与凸的分界点,则称(![]() ,f(
,f(![]() ))为曲线y=f(x)的拐点。
))为曲线y=f(x)的拐点。
注:拐点(![]() ,f(
,f(![]() ))是曲线上的一点,它有横坐标和纵坐标,不要只把横坐标当成拐点。
))是曲线上的一点,它有横坐标和纵坐标,不要只把横坐标当成拐点。
存在条件
必要条件
设函数f(x)在点![]() 的某邻域内具有二阶连续导数,若(
的某邻域内具有二阶连续导数,若(![]() ,f(
,f(![]() ))是曲线的拐点,则
))是曲线的拐点,则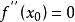 ,但反之不成立。
,但反之不成立。
第一充分条件
直接根据拐点的定义,可以得到曲线存在拐点的第一充分条件。
设函数f(x)在点![]() 的某邻域内具有二阶连续导数,若
的某邻域内具有二阶连续导数,若![]() 的两侧
的两侧![]() 异号,则(
异号,则(![]() ,f(
,f(![]() ))是曲线y=f(x)的一个拐点;若
))是曲线y=f(x)的一个拐点;若![]() 的两侧
的两侧![]() 同号,则(
同号,则(![]() ,f(
,f(![]() ))不是曲线的拐点。
))不是曲线的拐点。
第二充分条件
设函数y=f(x)在点![]() 处
处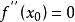 ,但
,但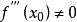 ,那么存在
,那么存在![]() 的一个领域,在该领域内
的一个领域,在该领域内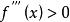 或
或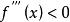 ,根据函数单调性判定定理,则在该邻域内
,根据函数单调性判定定理,则在该邻域内![]() 单调递增或
单调递增或![]() 单调递减,而
单调递减,而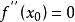 ,故存在点
,故存在点![]() 的一个邻域,在点
的一个邻域,在点![]() 的两侧
的两侧![]() 异号,从而判定
异号,从而判定![]() 为曲线y=f(x)的拐点的横坐标。根据以上分析,可以得到曲线存在拐点的第二充分条件。
为曲线y=f(x)的拐点的横坐标。根据以上分析,可以得到曲线存在拐点的第二充分条件。
若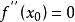 ,且
,且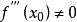 ,则(
,则(![]() ,f(
,f(![]() ))是曲线y=f(x)的拐点。
))是曲线y=f(x)的拐点。
除上述情况外,f(x)的二阶导数不存在的点也有可能是![]() 的符号发生变化的分界点。
的符号发生变化的分界点。
拐点的求法
可以按下列步骤来判断区间I上的连续曲线y=f(x)的拐点:
⑴求f''(x);
⑵令f''(x)=0,解出此方程在区间I内的实根,并求出在区间I内f''(x)不存在的点;
⑶对于⑵中求出的每一个实根或二阶导数不存在的点![]() ,检查f''(x)在
,检查f''(x)在![]() 左右两侧邻近的符号,那么当两侧的符号相反时,点(
左右两侧邻近的符号,那么当两侧的符号相反时,点(![]() ,f(
,f(![]() ))是拐点,当两侧的符号相同时,点(
))是拐点,当两侧的符号相同时,点(![]() ,f(
,f(![]() ))不是拐点。
))不是拐点。



 求购
求购

