- 电毛细现象
电毛细现象
电极界面上的界面张力(界面
自由能)与界面两侧的过剩
电荷密度以及界面上离子和分子的吸附量有关,并影响与此相关的
毛细管现象,称为电毛细现象。
用热力学方法处理电毛细现象所依据的基本公式是包含界面
自由能变化项的 吉布斯-杜亥姆公式:
SdT-Vdp+Adσ nidμi=0 (1)
式中S为熵;V为体积;A为面积;ni为 分子数;σ为界面自由能;μi为i粒子的 化学势。当温度T和压力 p不变时上式简化为:
dσ+γidμi=0 (2)
γi=ni/A,为i粒子的界面吸附量。习惯上常选取参考界面使溶剂的 表面吸附量为0,对于电极中的电子,ne-dμe=qdE,则式(2)可改写为:
dσ=-qdE-γidμi (3)
式中 q为电极金属一侧的过剩电荷密度;E 为 电极电势 (位);最后一项只累计溶液中除溶剂分子外的粒子。式(3)主要用于两种情况:
在保持溶液组成不变时,测量界面张力随电极电势的变化,为此常采用 毛细管静电计。此时上式简化为:
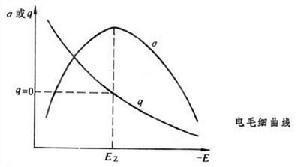
此式称为 李普曼公式。据此可以利用电毛细曲线,即σ-E 关系曲线(见图)的斜率来计算电极表面上的过剩电荷密度。例如在σ-E 曲线的最高点所反映的 q值为0,与此相应的电极电势称为零电荷电势Ez。在Ez左侧的电势区域内而q>0,即电极上带有正的过剩电荷。同理,在Ez右侧的电势区域内
SdT-Vdp+Adσ nidμi=0 (1)
式中S为熵;V为体积;A为面积;ni为 分子数;σ为界面自由能;μi为i粒子的 化学势。当温度T和压力 p不变时上式简化为:
dσ+γidμi=0 (2)
γi=ni/A,为i粒子的界面吸附量。习惯上常选取参考界面使溶剂的 表面吸附量为0,对于电极中的电子,ne-dμe=qdE,则式(2)可改写为:
dσ=-qdE-γidμi (3)
式中 q为电极金属一侧的过剩电荷密度;E 为 电极电势 (位);最后一项只累计溶液中除溶剂分子外的粒子。式(3)主要用于两种情况:
在保持溶液组成不变时,测量界面张力随电极电势的变化,为此常采用 毛细管静电计。此时上式简化为:
此式称为 李普曼公式。据此可以利用电毛细曲线,即σ-E 关系曲线(见图)的斜率来计算电极表面上的过剩电荷密度。例如在σ-E 曲线的最高点所反映的 q值为0,与此相应的电极电势称为零电荷电势Ez。在Ez左侧的电势区域内而q>0,即电极上带有正的过剩电荷。同理,在Ez右侧的电势区域内
 电毛细现象
电毛细现象
当电极电势不变时,测定溶液中某一组分浓度变化所起的界面张力变化,然后按下式计算该组分相对于溶剂分子的界面吸附量: 式中R为
气体常数;T为
热力学温度;ci为浓度。此式主要用来测定分子的吸附量。由于不可能单独改变某一离子的浓度和化学势,计算离子吸附量的公式要复杂一些。
根据电毛细现象,可以解释为什么电极电势常能影响电极表面的某些性质,如溶液 对电极表面的润湿能力、电极上气泡的附着情况、电极的 表面硬度以及溶液中电极与涂料和 粘结剂之间的粘合能力等。通过调节电极电势和采用适当的界面 活性物质(易于在界面上吸附的物质),可以人为地控制这类界面性质。
根据电毛细现象,可以解释为什么电极电势常能影响电极表面的某些性质,如溶液 对电极表面的润湿能力、电极上气泡的附着情况、电极的 表面硬度以及溶液中电极与涂料和 粘结剂之间的粘合能力等。通过调节电极电势和采用适当的界面 活性物质(易于在界面上吸附的物质),可以人为地控制这类界面性质。

相关百科
-
如何看待汽车价格 如何看待汽车降价后又涨价的现象呢?
2025-09-14 22:28:56 查看详情 -
如何看待年后汽车价格趋势 如何看待汽车降价后又涨价的现象呢?
2025-09-14 22:28:56 查看详情 -
如何确定汽车价格上涨了 如何理解汽车降价后的涨价现象?
2025-09-14 22:28:56 查看详情 -
发动机漏油 发动机表面有漏油现象,严重吗?
2025-09-14 22:28:56 查看详情 -
汽车同步器坏了有什么现象
2025-09-14 22:28:56 查看详情


 求购
求购





