公倍数

这些公倍数中最小的，就称为这些 整数的 最小公倍数（lowest common multiple）

。

 《求三个数的最小公倍数》其教学重点是让学生学会求三个数的最小公倍数的方法，难点是让学生理解三个数的最小公倍数的组成，即由三个数公有的质因数、两个数公有的质因数和各自独有的质因数相乘。这个难点不太容易突破。在平时教学中，经常见到大部分老师回避了教学难点，仅仅采用传统的“独白”方式，告诉学生怎样去求 最小公倍数，而后通过巩固练习让学生熟练掌握该方法。在这个过程中学生的学习是被动的，学生的思维没有得以充分的激活。真正的教育不是直接“告诉”，有意义的知识是学生在具体情境中通过活动体验而自主建构的．

A和B A/B=C　如果A能被B整除，则A为B和C的公倍数　两个数A和B，它们的公倍数就是既是A的倍数又是B的倍数的数，即能同时被A、B整除的数 　比如说：12和15，它们的公倍数是60，120，180，等等 　在这些公倍数中最小的那一个就叫最小公倍数，就是60。

公倍数

首先把两个数的质因数写出来，最小公倍数等于这两个数全部共有的质因数的代表与各自独有的质因数的乘积。

比如求45和30的最小公倍数。

45=3×3×5

30=2×3×5

30与45共有的质因数是1个3和1个5,而30和45独有的质因数分别是 3和2。即，

最小公倍数等于2×3×3×5=90

又如计算36和270的最小公倍数

36=2×2×3×3

270=2×3×3×3×5

36与270都有的质因数是1个2和2个3，而36独有质因数2，270独有质因数3和5。

最小公倍数等于2×2×3×3×3×5=540

如果较大数是较小数的倍数，较大数就是它们的最小公倍数。

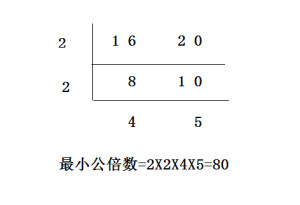
有一些砖,长宽高分别是15、12、6,请问怎样摆,才能够摆成一个最小的正方体.

解：设15、12、6的最小公倍数是60,所以最小的正方体棱长为60.

60÷15=4

60÷12=5

60÷6=10

答： 长：4块，宽：5块，高：10块，才能摆成一个最小的正方体。

公倍数(3)小数是不存在最大公因数和最小公倍数的，最大公因数（最大公约数）和最小公倍数只存在于自然数中。