模糊聚类分析

涉及事物之间的模糊界限时按一定要求对事物进行分类的数学方法。聚类分析是数理统计中的一种多元分析 方法，它是用数学方法定量地确定样本的亲疏关系，从而客观地划分类型。事物之间的界限，有些是确切的，有些则是模糊的。例人群中的面貌相像程度之间的界限是模糊的，天气阴、晴之间的界限也是模糊的。当聚类涉及事物之间的模糊界限时，需运用模糊聚类分析方法。模糊聚类分析广泛应用在气象预报、地质、农业、林业等方面。通常把被聚类的事物称为样本，将被聚类的一组事物称为样本集。模糊聚类分析有两种基本方法： 系统聚类法和逐步聚类法。^[1]

数据分类中，常用的分类方法有多元统计中的 系统聚类法、模糊聚类分析等.在模糊聚类分析中，首先 要计算模糊 相似矩阵，而不同的模糊相似矩阵会产生不同的分类结果;即使采用相同的模糊相似矩阵，不同的阈值也会产生不同的分类结果.“如何确定这些分类的有效性”便成为模糊聚类的要点。

识别研究中的一个重要问题.文献,把有效性不满意的原因归结于数据集几何结构的不理想.但笔者认为，不同的几何结构是对实际需要的反映，我们不能排除实际需要而追求所谓的“理想几何结构”，不理想的分类不应归因于数据集的几何结构.针对同一模糊 相似矩阵，文献建立了确定模糊聚类有效性的方法.用固定的显著性水平，在不同分类的F一统计量和F检验临界值的差中选最大者，即为有效分类.但是，当显著性水平变化时，此方法的结果也会变化.文献引进了一种模糊划分嫡来评价模糊聚类的有效性，并人为规定当两类的嫡大于一数时，此两类可合并，通过逐次合并，最终得到有效分类.此方法人为干预较多，当这个规定数不同时，也会得到不同的结果.另外这两种方法也未比较不同模糊相似矩阵的分类结果.

系统聚类法是基于模糊等价关系的模糊聚类分析法。在经典的聚类分析方法中可用经典 等价关系对样本集 进行聚类。设 是 上的经典 等价关系。对 中的两个元素 和 ，若 或( )∈ ，则将 和 并为一类，否则 和 不属于同一类。

相应地，可用 上的模糊 等价关系对样本集 进行模糊聚类。设 是 上的模糊 等价关系，是 的 隶属函数。对于任何 ∈【0，1】，定义 的 截关系 是 上的经典等价关系。根据 得到 的一种聚类,称为在 水平上的聚类。

应用这种方法,分类的结果与 的取值大小有关。 取值越大,分的 类数越多。 小到某一值时, 中的所有样本归并为一类。这种方法的优点在于可按实际需要选取 的值，以便得到恰当的分类。

系统聚类法的步骤如下：

①用数字描述样本的特征。设被聚类的样本集为 ={ 1，…, }。每个样本均有 种特征,记作 =( 1，…， )； =1，2，…, ； 表示描述样本 的第 个特征的数。　 ②规定样本之间的 相似系数 (0≤ ≤1； =1，…， )。 描述样本 与 之间的差异或相似的程度。 越接近于1,表明样本 与 之间的差异越小; 越接近于0，表明 与 之间的差异越大。 可用主观评定或集体评分的方 法规定，也可用公式计算，如采用夹角余弦法、最小最大法、算术平均最小法等。

因为 =1( 与自身没有差异), = ( 与 之间的差异等同于 与 之间的差异),所以由 ( =1，…， )可得 上的模糊相似关系。

一般， 不具备可传递性，因而 不一定是 上的模糊等价关系。

③运用合成运算 = ⋅ （或 = ⋅ 等）求出最接近相似关系 的模糊 等价关系 = （或 等）。若 已是模糊 等价关系，则取 = 。

④选取适当水平 （0≤ ≤1）,得到 的一种聚类。

逐步聚类法是一种基于模糊划分的模糊 聚类分析法。它是预先确定好待分类的样本应分成几类，然后按最优化原则进行 再分类，经多次迭代直到分类比较合理为止。

在分类过程中可认为某个样本以某一隶属度隶属于某一类，又以另一隶属度隶属于另一类。 这样，样本就不是明确地属于或不属于某一类。若样本集有 个样本要分成c类，则它的模糊划分 矩阵为此c× 模糊划分矩阵有下列特性：① ∈【0，1】； =1，…，c； =1,…， 。②即每一样本属于各类的隶属度之和为1。③即每一类模糊子集都不是空集。

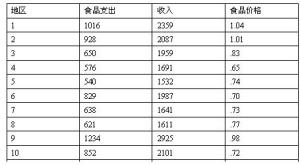模糊划分 矩阵有无穷多个，这种模糊划分矩阵的全体称为模糊划分空间。最优分类的标准是样 本与聚类中心的距离平方和最小。因为一个样本是按不同的隶属度属于各类的，所以应同时考虑它与每一类的聚类中心的距离。逐步聚类法需要反复 迭代计算，计算工作量很大，要在电子计算机上进行。算出最优模糊划分 矩阵后，还必须求得相应的常规划分。此时可将得到的聚类中心存在计算机中，将样本重新逐个输入，去与每个聚类中心进行比较，与哪个聚类中心最接近就属于哪一类。

这种方法要预先知道分类数，如分类数不合理，就重新计算。这就不如运用基于模糊 等价关系的 系统聚类法，但可以得到聚类中心，即各类模式样本，而这往往正是所要求的。因此可用模糊 等价关系所得结果作为初始分类，再通过反复 迭代法求得更好的结果。