- 双曲正切函数

双曲正切函数
基础定义
双曲正切函数(tanh)的定义与三角函数十分类似,它也是双曲正弦函数(sinh)与双曲余弦函数(cosh)的商[2]。定义式为: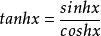 。
。
由于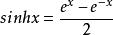 ,
,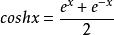 ,那么双曲正切函数的定义式为:
,那么双曲正切函数的定义式为:
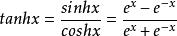
定义域
双曲正切的定义域为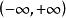 。[3]
。[3]
我们也可以推导出来:由于双曲正切函数定义式的分母是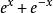 ,根据高中课本里的基本不等式:
,根据高中课本里的基本不等式:
![]() 双曲正切函数得出
双曲正切函数得出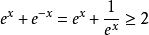
可见,双曲余弦函数的分母永远为正,不可能为零,则得出了该函数的定义域。
值域和有界性
双曲正切函数的图形夹在水平直线y=1及y=-1之间,且当x的绝对值很大时,它的图形在第一象限内接近于直线y=1,而在第三象限内接近于直线y=-1。[3]
即双曲正切函数的值域是(-1,1)。
证明: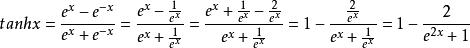
当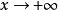 时,由于
时,由于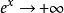 ,则
,则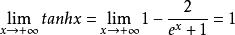 。
。
当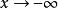 时,由于
时,由于![]() ,则
,则 。
。
奇偶性
双曲正切函数是奇函数,它的图形通过原点且关于原点对称。[3]
下面是证明:首先明确双曲正切函数的定义域是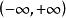 。
。
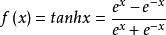 。
。
而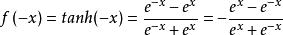
得出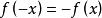 ,则证明出双曲正切函数为奇函数。
,则证明出双曲正切函数为奇函数。
周期性
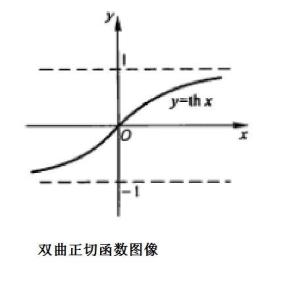 双曲正切函数的图像无论是双曲正切函数y=tanhx,还是双曲正弦函数y=sinhx、双曲余弦函数y=coshx,它们都不是周期函数。[4]
双曲正切函数的图像无论是双曲正切函数y=tanhx,还是双曲正弦函数y=sinhx、双曲余弦函数y=coshx,它们都不是周期函数。[4]
单调性
双曲正切函数在区间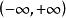 内是单调增加的。[3]
内是单调增加的。[3]
证明如下:
对双曲正切函数求导。
![]() 双曲正切函数
双曲正切函数
而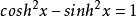
得出双曲正切函数的导数为: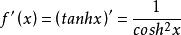 。而无论x取何值,双曲余弦函数的值始终大于等于1,得出x在
。而无论x取何值,双曲余弦函数的值始终大于等于1,得出x在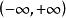 内大于0,单调递增。
内大于0,单调递增。
凹凸性
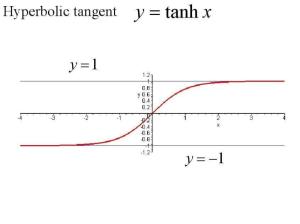 双曲正切函数的图像
双曲正切函数的图像
双曲正切函数在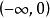 上是凹函数,在
上是凹函数,在![]() 上是凸函数[4]。
上是凸函数[4]。
根据定理:设f(x)在[a,b]上连续,在(a,b)内具有一阶和二阶导数,那么
(1)若在(a,b)内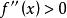 ,则f(x)在[a,b]上的图形是凹的。
,则f(x)在[a,b]上的图形是凹的。
(2)若在(a,b)内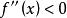 ,则f(x)在[a,b]上的图形是凸的。
,则f(x)在[a,b]上的图形是凸的。
则给双曲余弦函数二次求导,得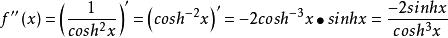
而双曲余弦函数恒大于0,而双曲正弦函数在x<0时,它的值小于0,x>0时,它的值大于0,即得出上述结论。
公式
除了双曲正切函数的定义式外,双曲正切函数还有以下式子。
1、和角公式: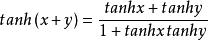
2、差角公式: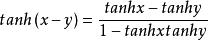 (和角公式的推导)
(和角公式的推导)
3、二倍角公式: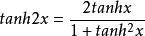 (和角公式的推导)
(和角公式的推导)
4、恒等式: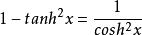
导数
双曲的导数是双曲余弦的平方的倒数。即:
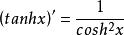 这与三角正切的导数相类似。
这与三角正切的导数相类似。
积分
双曲正切函数的积分[5]是:
![]() 双曲正切函数其中,大写的C为任意常数。另外,还有关于双曲正切函数的积分公式:
双曲正切函数其中,大写的C为任意常数。另外,还有关于双曲正切函数的积分公式:
![]() 双曲正切函数其中,小写的c为任意一个实数,是左边式子中x前的系数。
双曲正切函数其中,小写的c为任意一个实数,是左边式子中x前的系数。
泰勒展开式
双曲正切函数的泰勒展开式为[3]:
![]() 双曲正切函数可化为:
双曲正切函数可化为: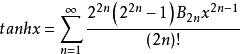
其中,![]()
反函数
 反双曲正切函数的图像双曲正切函数的反函数是反双曲正切函数,记作artanhx。它的定义式[5]为:
反双曲正切函数的图像双曲正切函数的反函数是反双曲正切函数,记作artanhx。它的定义式[5]为:
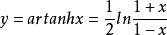
这函数的定义域为开区间(-1,1),它在开区间(-1,1)内是单调增加的奇函数,它的图形关于原点对称。



 求购
求购









