- 反双曲函数

反双曲函数
定义
我们知道,三角函数分为sin(正弦)、cos(余弦)、tan(正切)、cot(余切)、sec(正割)、csc(余割)六种。而双曲函数也如此。故而,反双曲函数也有六种。有反双曲正弦、反双曲余弦、反双曲正切、反双曲余切、反双曲正割、反双曲余割六种。这里,就介绍比较常见的前三种:反双曲正弦、反双曲余弦、反双曲正切。
反双曲函数是双曲函数的反函数。记为(arsinh、arcosh、artanh等等)。与反三角函数不同之处是它的前缀是ar意即area(面积),而不是arc(弧)。
反双曲正弦
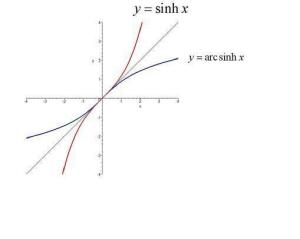 反双曲正弦函数图像反双曲正弦函数记作y=arsinhx。
反双曲正弦函数图像反双曲正弦函数记作y=arsinhx。
双曲函数y=sinhx的定义是y=sinhx=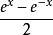 .那么,取它的反函数,最终得到反双曲正弦函数的定义是y=arsinhx=
.那么,取它的反函数,最终得到反双曲正弦函数的定义是y=arsinhx=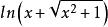 。
。
反双曲正弦函数的定义域为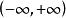 。它是奇函数。在区间
。它是奇函数。在区间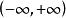 内单调增加。反双曲正弦函数的图像如图所示。
内单调增加。反双曲正弦函数的图像如图所示。
反双曲正弦函数的导数是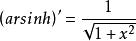 。不定积分是
。不定积分是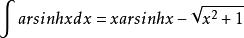 (不包含不定积分特有的常数C)。
(不包含不定积分特有的常数C)。
反双曲正弦函数的幂级数展开式是:
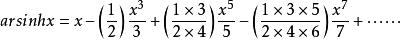
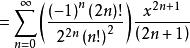 。
。![]()
反双曲余弦
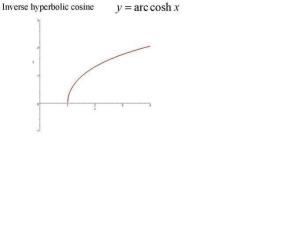 反双曲余弦函数图像反双曲余弦函数记作y=arcoshx。
反双曲余弦函数图像反双曲余弦函数记作y=arcoshx。
双曲函数y=coshx的定义是y=coshx=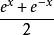 .那么,取它的反函数,最终得到反双曲余弦函数的定义是y=arcoshx=
.那么,取它的反函数,最终得到反双曲余弦函数的定义是y=arcoshx=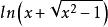 。
。
反双曲余弦函数的定义域为![]() 。它是非奇非偶函数。在区间
。它是非奇非偶函数。在区间![]() 内单调增加。反双曲余弦函数的图像如图所示。
内单调增加。反双曲余弦函数的图像如图所示。
反双曲余弦函数的导数是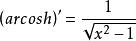 。不定积分是
。不定积分是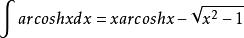 (不包含不定积分特有的常数C)。
(不包含不定积分特有的常数C)。
反双曲余弦函数的幂级数展开式是:
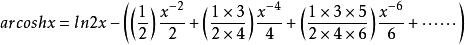
=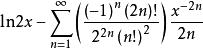 。
。![]()
反双曲正切
反双曲正切函数记作y=artanhx。
双曲函数y=sinhx的定义是y=tanhx=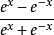 .那么,取它的反函数,最终得到反双曲正切函数的解析式是y=artanhx=
.那么,取它的反函数,最终得到反双曲正切函数的解析式是y=artanhx=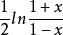 。
。
反双曲正切函数的定义域为![]() 。它是奇函数。在区间
。它是奇函数。在区间![]() 内单调增加。反双曲正切函数的图像如图所示。
内单调增加。反双曲正切函数的图像如图所示。
反双曲正切函数的导数是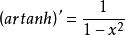 。不定积分是
。不定积分是 (不包含不定积分特有的常数C)。需要注意,在反双曲正切的不定积分中,有条件
(不包含不定积分特有的常数C)。需要注意,在反双曲正切的不定积分中,有条件![]() ,此不定积分才能成立。
,此不定积分才能成立。
反双曲正切函数的幂级数展开式是:
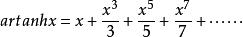
=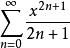 。
。![]()
对比
在数学中,双曲函数类似于常见的(也叫圆函数的)三角函数。基本双曲函数是双曲正弦“sinh”,双曲余弦“cosh”,从它们导出双曲正切“tanh”等。
求导
双曲函数求导
shx = (e^x - e^(-x)/2, (shx) ' =chx
chx = (e^x + e^(-x)/2, (chx) ' =shx
thx = shx / chx, (thx) ' = 1/(chx)^2
反双曲函数求导
arsinh x = ln[ x+ (x^2+1)^(1/2) ] , (arsinh x) ' = 1/ (x^2+1)^(1/2)
arcosh x = ln[ x+ (x^2-1)^(1/2) ] , (arcosh x) ' = 1/ (x^2-1)^(1/2)
artanh x =(1/2) [ ln(1+x)/(1-x) ], (artanh x) ' = 1/(1-x^2)



 求购
求购









