N色定理

1974年，德国数学家林格和美国数学家杨斯证明了，在曲面上作图，有以下定理：

,(参见《图论导引》214页，机械工业出版社；人民邮电出版社258页)

其中[X]表示整数部分，p表示洞的个数。

在平面中4个或者4个以下的区域

可以构成两两相连的区域，可以一笔划。

平面上4个区域两两相连图1图（1）。每个区域必须是单连通的，就是一个区域不能够是分成2块或者2块以上。这是著名的四色猜想。大家知道，平面上不可能有两两相通的5个区域。注意，两两相连是未来网络枢纽的要求。

在一个轮胎形状的环面的表面

7个或者7个以下的区域可以构成两两相连的区域。可以“一笔划”。

图（2）（右则）上下对折以后，再左右对折，形成一个轮胎状，7个区域两两相连（国外数学家给出）.两两相连的区域可以不经过其它区域到达任何一个区域。P。J希伍德以毕生精力研究四色定理，并且证明了5色定理，稀伍德考察了一般曲面着色问题提出一个推测：在有P>1个洞的封闭曲面上，足以为任何地图着色的最小数等于

背面。其中[X]表示整数部分，即图（2)

正面.

图2--7色定理。亏格1时有7个区域两两相连

在有2个洞的双环面

有8个区域两两相连（图3）

例如两个洞的曲面应该。（见图3右下图）王晓明王蕊珂经过9年完成。

注意，研究两两相连区域是因为网络战争的需要。在一个两两相连的枢纽，交通是不会堵塞的。

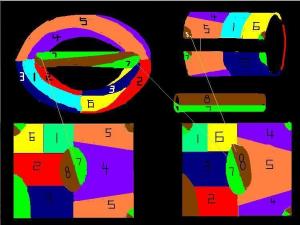图3--八色定理图片，构造用了9年下面的两个图是一回事，上下对折，再左右对折，就是一个轮胎形状，有6个区域两两相连，再把有区域7和区域8的管子安装到相应部位，就是一个有两个洞的曲面，有8个区域两两相连（上面是图片，下面是依据图片制作的模型，王晓明构造，制作模型，充分说明林格和杨斯的证明是正确的）。

正面

依据图片制作的模型正面

在有三个洞的曲面上

有9个区域两两相连（图4）

图4--亏格3时有9个区域两两相连是在图2的基础上（7个区域两两相连）加上一个三叉，下图三叉对应上图的相应位置，就是一个方向盘形状的亏格3的9个两两相连区域参见图5，.

王晓明构造（上面是图片，下面两个是依据图片制作的模型）。

背面

九色图片模型

亏格为4时

有10个两两相连区域（图5）

参见图5：

图5--4个洞的10个两两相连区域图5在图2的基础上，上图上下对折，再左右对折成为一个轮胎形状，下图四叉按照ABCD位置对应上图，就是一个有4个洞的10个两两相连区域参见图6,因为林格证明

十色定理图片模型，王晓明完成（右边是依据图片制作模型，有10个区域两两相连）。

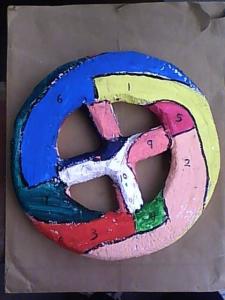背面

亏格5时11个区域两两相连

（图6）

有5个洞的曲面有11个区域两两相连参见图7，下面图上下对折再左右对折形成一个轮胎，有7个区域两两相连，把上面的五叉按照ABCD对应安装上去，就是一个有11个区域两两相连。林格1974年证明，。王晓明构造，湖南李恒嘉安装。

亏格7时有12个区域两两相连

12色定理。，参见图7，右上图是外环平面图，有6个区域两两相连，先上下对折，再左右对折，左右对折时一段轻轻扭转，使得1对着5,2对着6,3对着4。右下图和左下图是内环，上下对折再左右对折形成一个轮胎形状，左右对折时一端轻轻扭转，使得7对折11,8对着12,9对折10。外部有6根柱子与外环相连，形成一个有7个洞的12个区域两两相连，王晓明构造。

可以构造任意多个两两相连区域

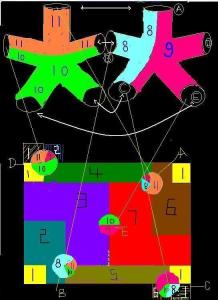
现在有两根管子，一个记为1，一个记为2，它们代表两个区域。我们假定所有的管子都是可以随意拉伸和弯曲的。把两根管子端端相连，就是一个汽车轮胎一样的环，它有两个区域，我们再用一根直管子记为3，安在这个环的中间，一头连着区域1，一头连着区域2，现在它是有两个洞的双环了，有三个区域两两相连。
现在我们用一个“丁”字型的三叉管，记为区域4，三个端口分别与区域1，区域2，区域3相连。于是现在有4个区域两两相连；
我们再用一根四叉管记为区域5,4个端口分别与区域1,2,3,4相连，现在有5个区域两两相连。
这个步骤可以无限制进行下去，用五叉管，六叉管，。.。构造无穷多个区域，它们都是两两相连的。

无穷多个两两相连区域的具体构造方法

有无穷多个区域两两相连，与有无穷多个素数两两互素，我们可以把图论与数论联系起来。用数论解决图论，或者反之

可以构造任意多个两两相连区域

现在有两根管子，一个记为1，一个记为2，它们代表两个区域。我们假定所有的管子都是可以随意拉伸和弯曲的。把两根管子端端相连，就是一个汽车轮胎一样的环，它有两个区域，我们再用一根直管子记为3，安在这个环的中间，一头连着区域1，一头连着区域2，现在它是有两个洞的双环了，有三个区域两两相连。
现在我们用一个“丁”字型的三叉管，记为区域4，三个端口分别与区域1，区域2，区域3相连。于是现在有4个区域两两相连；
我们再用一根四叉管记为区域5,4个端口分别与区域1,2,3,4相连，现在有5个区域两两相连。
这个步骤可以无限制进行下去，用五叉管，六叉管，。.。构造无穷多个区域，它们都是两两相连的。

无穷多个两两相连区域的具体构造方法

有无穷多个区域两两相连，与有无穷多个素数两两互素，我们可以把图论与数论联系起来。用数论解决图论，或者反之。

与哥德巴赫猜想和费马大定理的关系

数学家和物理学家把上面（第八节中的）这个叫做岐管。
在数论中，最重要的元素就是素数，欧几里得证明了有无穷多个素数，并且它们有一个特点就是两两互素。无穷多个两两互素的素数与无穷多个两两相连区域一一对应。
就是说用这个方法把数论与图论联系起来，这个方法的意图叫做朗兰兹纲领。
区域1，代表第一个素数2，第二个区域代表第二个素数3，。.，第n个区域代表第n个素数。
我们把这个第八节图中的岐管倒过来，就像一个网子，篮球网子。篮球网子是把篮球往里面投。

岐管或者称为筛子

公元前300年古希腊有一个数学家叫做埃拉特斯特尼，他把这个网子当成筛子，把自然数往里面扔，他说凡是合数通过筛子以后就会从网子里面筛掉，留下的是素数，这个就是著名的埃拉特斯特尼筛法。

我们上面这个岐管筛子是把偶数往里面扔，哥德巴赫说，大于4的偶数一个也不会漏出筛子，除了6=3+3以外，其他偶数都是可以在不同的素数区域被拦截。例如8会在区域2也就是素数3和素数5（第三个区域）被拦截；偶数10会在素数3和素数7的两个区域之间被拦截；。.。总之，无穷多个偶数都逃不脱这个网子，没有一个偶数可以漏到外面去。（右图）
看到没有？数论与图论已经融合一起了。
这个还不算神奇，这个岐管的内部空间我们记为X，外部空间记为Y，它有很多洞,可以有无穷多个洞，可以有无穷多个空间维度n，宇宙内外整体记为1，就是说Xⁿ+Yⁿ=1，这个叫做费马曲线，它是由费马大定理Aⁿ+Bⁿ=Cⁿ同时除以Cⁿ得到的。
费马大定理与哥德巴赫猜想联系起来了。右边就是费马大定理的岐管[1]。

费马大定理中的岐管

费马大定理的岐管就是m理论岐管

物理学家认为，宇宙是10维空间或者11维空间，或者26维空间等5个版本。还有物理学家认为有无穷多个维度的空间。他们管这个理论叫做玄理论或者M理论，是把广义相对论与量子理论结合一起的终极理论，霍金说是最后的理论。

在弦/m理论的11维空间里，有4维空间的伸展，7维空间卷缩起来的。 几何体的拓扑性质同粒子紧密相关。例如，这种粒子几何体有几个洞，决定着粒子世代的数目，在这些卷缩维度的空间里所采取的几何构型决定着弦或者膜能够有什么样的震动模式，从而决定着各种粒子的质量、自旋、以及电荷等各种相互作用的耦合常数。

原来，不仅仅自旋和同位旋等内部变量和内部空间都出自这些多维空间的几何学，而且粒子的电荷质量等性质，无一不是从这里产生出来的，不仅仅如此，甚至我们生活本身也通过三维空间和一维时间都是从类似的几何体的构造中生长出来的。 我们生活在高维宇宙的一小片中，大到银河宇宙，小至原子夸克，都是 弦线构成的。

与爱因斯坦方程的联系

质能方程E=mc²，E表示能量，m代表质量，而c则表示光速。在上面的岐管表面是C，它的平方就是光速扫过的面积。这个费马方程岐管，弦/m理论高维空间认为这个面团里面是空心的，就是说，这个面团戳了一些贯通的洞以后，再把面团内部看成一个空心的，这个曲面只是一个没有厚度的膜。