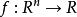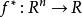- 共轭函数

共轭函数
定义
设函数,定义函数为
 此函数称为函数
此函数称为函数![]() 的共轭函数。使上述上确界有限,即差值
的共轭函数。使上述上确界有限,即差值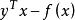 在
在![]() 有上界的所有
有上界的所有![]() 构成了共轭函数的定义域。图1描述了此定义。
构成了共轭函数的定义域。图1描述了此定义。
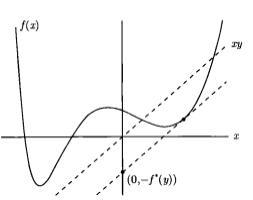 图1
图1
图1中,函数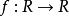 以及某一
以及某一![]() 。共轭函数
。共轭函数![]() 是线性函数
是线性函数![]() 和
和![]() 之间的最大差值,见图中虚线所示。如果
之间的最大差值,见图中虚线所示。如果![]() 可微,在满足
可微,在满足 的点
的点![]() 处差值最大。[2]
处差值最大。[2]
显而易见,![]() 是凸函数,这是因为它是一系列
是凸函数,这是因为它是一系列![]() 的凸函数(实质上是仿射函数)的逐点上确界。无论f是否是凸函数,
的凸函数(实质上是仿射函数)的逐点上确界。无论f是否是凸函数,![]() 都是凸函数。(注意到这里当
都是凸函数。(注意到这里当![]() 是凸函数时,下标
是凸函数时,下标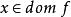 可以去掉,这是因为根据关于扩展值延伸的定义,对于
可以去掉,这是因为根据关于扩展值延伸的定义,对于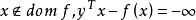 )。
)。
基本性质
Fenchel不等式
从共轭函数的定义我们可以得到,对任意![]() 和
和![]() ,如下不等式成立
,如下不等式成立
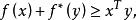 上述不等式即为Fenchel不等式(当
上述不等式即为Fenchel不等式(当![]() 可微的时候亦称为Young不等式)。[2]
可微的时候亦称为Young不等式)。[2]
以函数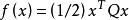 为例,其中
为例,其中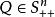 ,我们可以得到如下不等式
,我们可以得到如下不等式
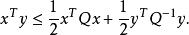
共轭的共轭
上面的例子以及“共轭”的名称都隐含了凸函数的共轭函数的共轭函数是原函数。也即:如果函数f是凸函数且f是闭的(即![]() 是闭集),则
是闭集),则![]() 。例如,若
。例如,若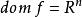 ,则我们有
,则我们有![]() ,即f的共轭函数的共轭函数还是f。
,即f的共轭函数的共轭函数还是f。
可微函数
可微函数f的共轭函数亦称为函数f的Legendre变换。(为了区分一般情况和可微情况下所定义的共轭,一般函数的共轭有时称为Fenchel共轭。)[2]
设函数f是凸函数且可微,其定义域为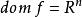 ,使
,使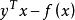 取最大的
取最大的![]() 满足
满足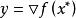 ,反之,若
,反之,若![]() 满足
满足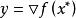 ,
,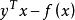 在
在![]() 处取最大值。因此,如果
处取最大值。因此,如果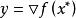 ,我们有
,我们有
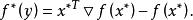 所以,给定任意y,我们可以求解梯度方程
所以,给定任意y,我们可以求解梯度方程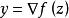 ,从而得到y处的共轭函数
,从而得到y处的共轭函数![]() 。
。
我们亦可以换一个角度理解。任选![]() ,令
,令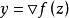 ,则
,则
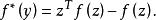
伸缩变换和复合仿射变换
若a>0以及b∈R,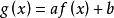 的共轭函数为
的共轭函数为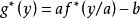 。
。
设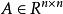 非奇异,
非奇异,![]() ,则函数
,则函数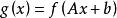 的共轭函数为
的共轭函数为
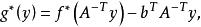 其定义域为
其定义域为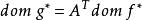 。[2]
。[2]
独立函数的和
如果函数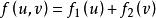 ,其中
,其中![]() 和
和![]() 是凸函数,且共轭函数分别为
是凸函数,且共轭函数分别为![]() 和
和![]() ,则
,则
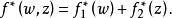 换言之,独立凸函数的和的共轭函数是各个凸函数的共轭函数的和。(“独立”的含义是各个函数具有不同的变量。)[2]
换言之,独立凸函数的和的共轭函数是各个凸函数的共轭函数的和。(“独立”的含义是各个函数具有不同的变量。)[2]
举例分析
考虑R上一些凸函数的共轭函数。[2]
仿射函数
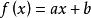 ,作为x的函数,当且仅当y=a,即为常数时
,作为x的函数,当且仅当y=a,即为常数时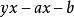 有界。因此,共轭函数
有界。因此,共轭函数![]() 的定义域为单点集
的定义域为单点集![]() ,且
,且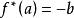 。
。
负对数函数
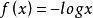 ,定义域为
,定义域为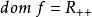 。当
。当![]() 时,函数
时,函数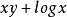 无上界,当y<0时,在
无上界,当y<0时,在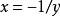 处函数达到最大值。因此,定义域为
处函数达到最大值。因此,定义域为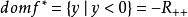 ,共轭函数为
,共轭函数为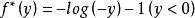 。
。
指数函数
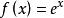 ,当
,当![]() 时,函数
时,函数![]() 无界。当y>0时,函数
无界。当y>0时,函数![]() 在
在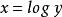 处达到最大值。因此
处达到最大值。因此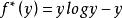 。当
。当![]() 时,
时,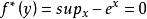 。综合起来,
。综合起来,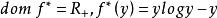 (我们规定
(我们规定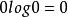 )。
)。
负熵函数
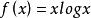 ,定义域为
,定义域为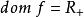 (同上面讨论,
(同上面讨论,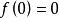 )。对所有 y,函数
)。对所有 y,函数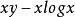 关于
关于![]() 在
在![]() 上有上界,因此
上有上界,因此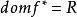 。在
。在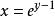 处,函数达到最大值。因此
处,函数达到最大值。因此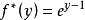 。
。
反函数
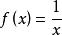 ,
,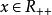 。当y>0时,
。当y>0时,![]() 无上界。当y=0时,函数有上确界0;当y<0时,在
无上界。当y=0时,函数有上确界0;当y<0时,在 处达到上确界。因此,
处达到上确界。因此,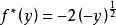 且
且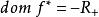 。[2]
。[2]

-
1641函数信号发生器
2025-09-29 17:15:28 查看详情


 求购
求购