- 形心

形心
定义
 形心(3)如果一个对象具有一致的密度,或者其形状和密度具有某种对称性足以确定几何中心,那么它的几何中心和质量中心重合,该条件是充分但不是必要的。
形心(3)如果一个对象具有一致的密度,或者其形状和密度具有某种对称性足以确定几何中心,那么它的几何中心和质量中心重合,该条件是充分但不是必要的。
有限个点总存在几何中心,可以通过计算这些点的每个坐标分量的算术平均值得到。这个中心是空间中一点到这有限个点距离的平方和的惟一最小值点。点集的几何中心在仿射变换下保持不变。
判断位置
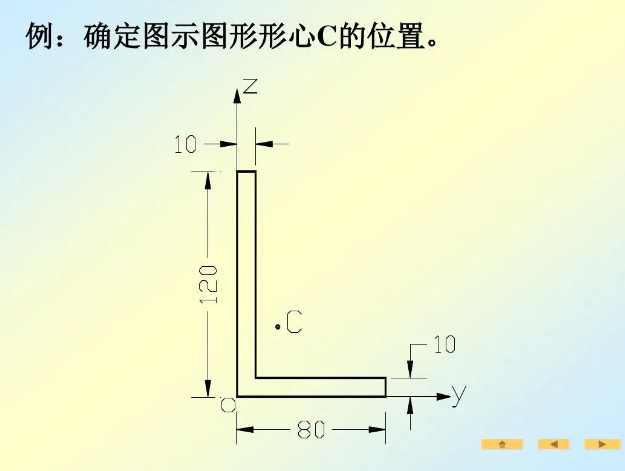
判断形心的位置:
当截面具有两个对称轴时,二者的交点就是该截面的形心。据此,可以很方便的确定圆形、圆环形、正方形。
 形心
形心
的形一个对称轴的截面,其形心一定在其对称轴上,具体在对称轴上的哪一点,则需计算才能确定。我们把均匀平面薄片的重心叫做这平面薄片所占的平面图形的形心。
性质
一个凸对象的几何中心总在其内部。一个非凸对象的几何中心可能在外部,比如一个环或碗的几何中心不在内部。
三角形的重心与三顶点连线,所形成的三个三角形面积相等。
顶点到重心的距离是中线的![]() 。
。
重心、外心、垂心、九点圆圆心四点共线。
重心、内心、奈格尔点、类似重心四点共线。
三角形的重心同时也是中点三角形的重心。
在直角座标系中,若顶点的座标分别为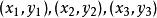 ,则中点的座标为:
,则中点的座标为:
![]()
三线坐标中、重心的座标为:
![]()
三角形的中心
形心是三角形的几何中心,通常也称为重心,三角形的三条中线(顶点和对边的中点的连线)交点,此点即为重心。[1]
四面体的中心
类似三角形的中心的结论对四面体也成立,四面体的几何中心是所有顶点和相对平面中心的连线的交点。这些线段被中心分成3:1。这个结论能自然推广到任何 n-维单形。如果单形的顶点集是 ,将这些顶点看成向量,几何中心位于:
,将这些顶点看成向量,几何中心位于:
![]()
多边形的中心
一个由N个顶点(xi, yi)确定的不自交闭多边形的中心能如下计算:[2]
记号( xN, yN)与顶点( x0, y0)相同。多边形的面积为:
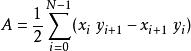
多边形的中心由下式给出:
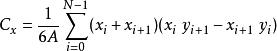
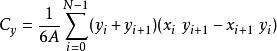
有限点集中心
给定有限点集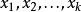 属于
属于![]() ,它们的中心定义 C为
,它们的中心定义 C为
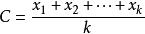 。
。
面积中心
面积中心和质量中心非常类似,面积中心只取决于图形的几何形状。如果物体是均匀的,质量中心将位于面积中心。
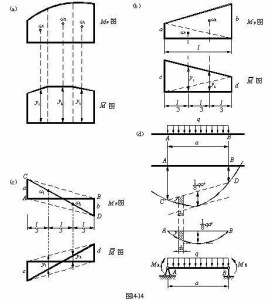
对于两部分组成的图形,将有如下等式: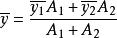
![]() 是特定部分的面积中心到所选参考系的距离。A是特定部分的面积。
是特定部分的面积中心到所选参考系的距离。A是特定部分的面积。
当一个复杂几何图形可以分成一些已知的简单几何图形时,先计算各部分的面积中心,然后通过下面一般的公式计算整个图形的面积中心:
![]()
![]()
这里从y-轴到中心的距离是![]() ,从x-轴到中心的距离是
,从x-轴到中心的距离是![]() ,中心的坐标是
,中心的坐标是![]() 。
。
锥的中心
圆锥或棱锥的中心位于连接顶点和底的中心的线段上,分比为3:1。
对称中心
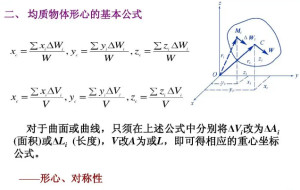 形心(3)如果中心确定了,那么中心是所有它对称群的不动点。从而对称能全部或部分确定中心,取决于对称的种类。另外可以知道,如果一个对象具有传递对称性,那么它的中心是不确定的或不在内部,因为一个传递变换群没有不动点。
形心(3)如果中心确定了,那么中心是所有它对称群的不动点。从而对称能全部或部分确定中心,取决于对称的种类。另外可以知道,如果一个对象具有传递对称性,那么它的中心是不确定的或不在内部,因为一个传递变换群没有不动点。
地理中心
地理学中,地球表面一个区域的几何中心也称为地理中心。



 求购
求购
