克拉珀龙方程

　　pV=nRT

　　推导该公式建立在Boyle-Marriote定律，Charles-Gay-Lussac定律，Avogadro定律基础上

　　V=f（p，T,N）

　　求V全微分

　　将Boyle-Marriote定律，以及Charles-Gay-Lussac定律代入全微分中

　　不定积分得到lnV+lnp=lnT+C

　　令C=lnR

　　即得pVm=RT

　　同乘以n得到pV=nRT

　　注：所有气体R值均相同。

　　如果压强、温度和体积都采用国际单位（SI），则P表示压强，单位Pa；V表示气体体积，单位立方米；n表示物质的量，单位mol；T表示热力学温度，单位K（开尔文）；R表示气体常数，单位J·mol^-1·K^-1或kPa·L·K^-1·mol^-1。R=8.314帕米3/摩尔·K。

　　因为n=m/M、ρ=m/v（n—物质的量，m—物质的质量，M—物质的摩尔质量，数值上等于物质的分子量，ρ—气态物质的密度），所以克拉伯龙方程式也可写成以下两种形式：

　　Pv=m/MRT　……②

　　PM=ρRT　……③

　　以A、B两种气体来进行讨论。

　　（1）在相同T、P、V时：

　　根据①式：nA=nB（即阿伏加德罗定律）

　　（2）在相同T·P时：　　摩尔质量之比=分子量之比=密度之比=相对密度）。若mA=mB则MA=MB。

　　体积之比=摩尔质量的反比；两气体的物质的量之比=摩尔质量的反比）

　　物质的量之比=气体密度的反比；两气体的体积之比=气体密度的反比）。

　　（3）在相同T·V时：

　　摩尔质量的反比；两气体的压强之比=气体分子量的反比）。

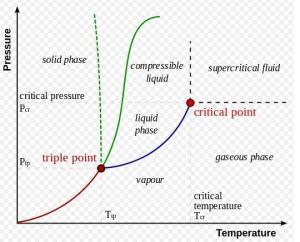典型的相图，途中的界限即为相平衡线

　　我们可以利用阿伏加德罗定律以及物质的量与分子数目、摩尔质量之间的关系得到以下有用的推论：

　　(1)同温同压时：①V1:V2＝n1:n2＝N1:N2

　　②ρ1:ρ2＝M1:M2

　　③ 同质量时：V1:V2＝M2:M1

　　(2)同温同体积时:　④ p1:p2=n1:n2＝N1:N2

　　⑤ 同质量时： p1:p2＝M2:M1

　　(3)同温同压同体积时: ⑥ ρ1:ρ2＝M1:M2＝m1:m2

　　具体的推导过程请大家自己推导一下，以帮助记忆。推理过程简述如下：

　　(1)、同温同压下，体积相同的气体就含有相同数目的分子，因此可知：在同温同压下，气体体积与分子数目成正比，也就是与它们的物质的量成正比，即对任意气体都有V=kn；因此有V1:V2=n1:n2=N1:N2，再根据n=m/M就有式②；若这时气体质量再相同就有式③了。

　　(2)、从阿伏加德罗定律可知：温度、体积、气体分子数目都相同时，压强也相同，亦即同温同体积下气体压强与分子数目成正比。其余推导同(1)。

　　(3)、同温同压同体积下，气体的物质的量必同，根据n=m/M和ρ=m/V就有式⑥。当然这些结论不仅仅只适用于两种气体，还适用于多种气体。

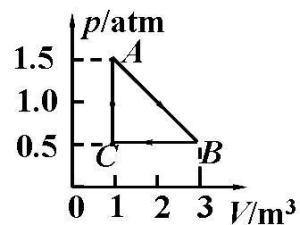克拉珀龙方程

　　在同温同压下，像在上面结论式②和式⑥中出现的密度比值称为气体的相对密度D=ρ1:ρ2=M1:M2。

　　注意：

　　①D称为气体1相对于气体2的相对密度，没有单位。如氧气对氢气的密度为16。

　　②.若同时体积也相同，则还等于质量之比，即D＝m1:m2。

值得注意的是，把理想气体方程和克拉伯龙方程等效是不正确的。一般克拉伯龙方程是指描述相平衡的方程dp/dT=L/(TΔV)。尽管理想气体定律是由克拉伯龙发现，但是国际上不把理想气体状态方程叫克拉伯龙方程。