- 三角方程组

三角方程组
三角函数方程组的解法原理
三角函数方程组的解法原理,与代数学中解方程组的方法类似:它们都是首先通过代数的或三角的变换, 逐渐消去未知数,直到化为含有唯一的未知量的普通方程并对它求解,然后再把这个解代入到其他各式中,求其全部解[2]。
解三角方程组的注意事项
解三角方程组时要注意以下四点:
1.消去三角方程组中的未知数,一般除了使用代入法外,还常常利用各种三角公式与代数变换。 特别地, 当问题有不同情况时,也常要求有不同的方法,这些并没有固定的规律可循,这是求解三角方程组的一个很大困难,克服这个图难的办法,要求三角公式运用熟练,多作题目,多见类型,逐步提高分析问题的能力。
2.求得方程组的解之后,与代数中解方程组一样, 也得一组一组地把解分别列出,并将所得的每组解一一代入到原方程组中进行检验,去掉增加根,并要注意遗根。代入检验是很麻烦的,一般方法是只把在区间![]() 上的角代入进行检验,而不把解的一般形式代入到方程组中,这样可使计算简单些[2]。
上的角代入进行检验,而不把解的一般形式代入到方程组中,这样可使计算简单些[2]。
3.所求得的解,有时还要求受到一定条件的约束,常见的情况有:
(1)当解中含有形如arcsin2或arcsin(-2)这样的项时,由于这样的项不可能代表任何确定的角,故应在说明之后舍去。
(2)当解中含有形如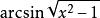 的项时,由于我们只在实数范围内讨论三角函数,显然必须满足条件
的项时,由于我们只在实数范围内讨论三角函数,显然必须满足条件
![]() 且
且
![]() 并由此求得x的取值范围。但是, 我们约定,只要题目中没有明确提出要求,我们并不进行讨论,即认为这样已经求得了最后结果。
并由此求得x的取值范围。但是, 我们约定,只要题目中没有明确提出要求,我们并不进行讨论,即认为这样已经求得了最后结果。
4.由于
![]() 所以, 当方程的系数为文字系数时,方程组解的形式往往随所采取的解法不同而有不同。但是,不管解的形式怎样,只要合理就行,并不需要化为一致。当方程的系数为普通数字时,我们也这样办,但遇到这种情况的机会要少一些[2]。
所以, 当方程的系数为文字系数时,方程组解的形式往往随所采取的解法不同而有不同。但是,不管解的形式怎样,只要合理就行,并不需要化为一致。当方程的系数为普通数字时,我们也这样办,但遇到这种情况的机会要少一些[2]。
例题解析
1.解方程组:
![]()
解:显然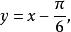
且
![]() 因为
因为
![]() (
(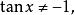 即
即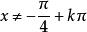 ),所以,从方程(1)得
),所以,从方程(1)得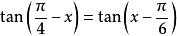 ,由此,
,由此,
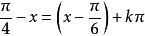 和
和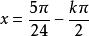 。
。
2.解方程组[2]:
![]()
解:由(1)得
![]() 使(3)代入(2)
使(3)代入(2)
![]()
![]() 所以
所以
![]()
使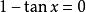 ,则
,则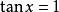 ,所以
,所以
![]() 代入(3)
代入(3)
![]()
使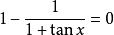 ,则
,则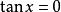 ,所以
,所以
![]() 代入(3),有
代入(3),有
![]()
答:方程组的解为
![]()

-
非线性方程组数值解法
2025-09-23 02:53:46 查看详情 -
F1方程赛车逆向设计
2025-09-23 02:53:46 查看详情 -
长江三角洲地区区域规划
2025-09-23 02:53:46 查看详情 -
三款小排量小型SUV雪铁龙C3 1.8L车型的油耗方程式
2025-09-23 02:53:46 查看详情 -
成都车展:一汽奔腾无限方程架构发布/第三代B70将问世 e
2025-09-23 02:53:46 查看详情


 求购
求购









