- 对勾函数
对勾函数
函数定义
对勾函数对勾函数是指形如
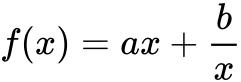（ab>0)的函数.
性质
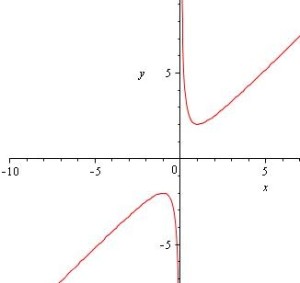
图像
对勾函数的图像是分别以y轴和y=ax为渐近线的两支曲线，且图像上任意一点到两条渐近线的距离之积恰为渐近线夹角的正弦值与|b|的乘积.
若a>0,b>0, 在第一象限内，其转折点为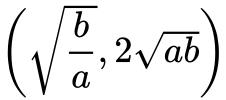
.
最值
当定义域为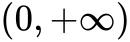
时，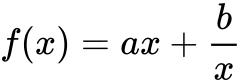
（a>0, b>0)在
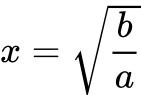处取最小值，最小值为
.
当定义域为
时，该函数无最值，
当定义域为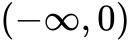
时，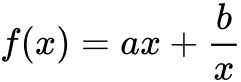
（a>0,b>0）在
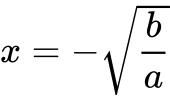处取最大值，最大值为
。
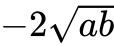奇偶单调性
奇偶性
对勾函数是奇函数.
单调性
令k=
，那么：
增区间：{x|x≤-k}和{x|x≥k}；减区间：{x|-k≤x<0}和{x|0<x≤k}
变化趋势：在y轴左边先增后减，在y轴右边先减后增.
推导过程
1导数法
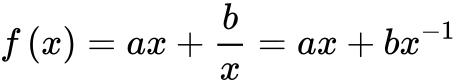
求导得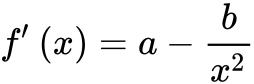
令f'(x)=0，计算得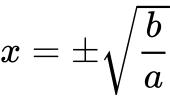
即对勾函数的转折点横坐标分别为
,
.
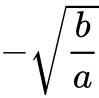2均值不等式法
当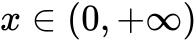
时，
由均值不等式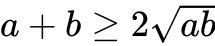
,(a>0,b>0)
将中
看做a，
看做b代入上式，得
当且仅当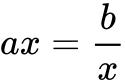
,即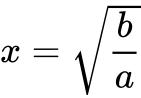
时等号成立.
故当x>0时，对勾函数的转折点横坐标为
.
相关百科
-
-
-
-
-
-
-
-
-
-
1641函数信号发生器
2025-09-21 05:00:14 查看详情
求购