- 标量场

标量场
定义
当研究物理系统中温度、压力、密度等在一定空间内的分布状态时,数学上只需用一个代数量来描绘,这些代数量(即标量函数)所定出的场就称为数量场,也称标量场。[1]最常用的标量场有温度场,电势场,密度场,浓度场等等[2]。
标量场的等值面
定义
一个标量场![]() 可以用一个标量函数来表示。在直角坐标系中,可将
可以用一个标量函数来表示。在直角坐标系中,可将![]() 表示为
表示为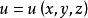 。
。
令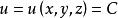 ,其中
,其中![]() 是任意常数,则该式在几何上表示一个曲面,在这个曲面上的各点,虽然坐标
是任意常数,则该式在几何上表示一个曲面,在这个曲面上的各点,虽然坐标![]() 不同,但函数值相等,称此曲面为标量场
不同,但函数值相等,称此曲面为标量场![]() 的等值面。随着
的等值面。随着![]() 的取值不同,得到一系列不同的等值面。同理,对于由二维函数
的取值不同,得到一系列不同的等值面。同理,对于由二维函数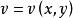 所给定的平面标量场,可按
所给定的平面标量场,可按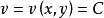 得到一系列不同值的等值线。
得到一系列不同值的等值线。
作用
标量场的等值面或等值线,可以直观地帮助我们了解标量场在空间中的分布情况。例如,根据地形图上等高线及其所标出的高度,我们就能了解到该地区的高低情况,根据等高线分布的疏密程度可以判断该地区各个方向上地势的陡度。[3]
标量场的方向导数
定义
设![]() 为标量场
为标量场 中的一点,从
中的一点,从![]() 出发引出一条射线
出发引出一条射线![]() ,在
,在![]() 上
上![]() 点附邻取一点
点附邻取一点![]() ,记线段
,记线段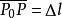 ,如果当
,如果当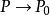 时,
时,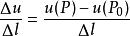 的极限存在,则称它为函数
的极限存在,则称它为函数![]() 在点
在点![]() 处沿
处沿![]() 方向的方向导数,记作:
方向的方向导数,记作:
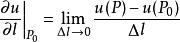
由此定义可知,方向导数是函数![]() 在一点处沿某一方向对距离的变化率,故当
在一点处沿某一方向对距离的变化率,故当![]() 时,
时,![]() 沿
沿![]() 方向是增加的;当时
方向是增加的;当时![]() ,
,![]() 沿
沿![]() 方向是减少的。[3]
方向是减少的。[3]
方向导数的计算
在直角坐标系中,设函数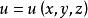 在
在 处可微,则有:
处可微,则有:
在上式中,当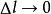 时,有
时,有![]() 。
。
将上式两边同除以![]() 并取极限得到
并取极限得到![]() 方向导数的计算公式:
方向导数的计算公式:
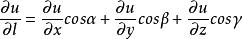
在上式中,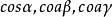 为方向
为方向![]() 的方向余弦。[3]
的方向余弦。[3]
标量场的梯度
定义
方向导数为我们解决了函数![]() 在给定点处沿着某个方向的变化率问题。然而从场中的给定点
在给定点处沿着某个方向的变化率问题。然而从场中的给定点![]() 出发,标量场
出发,标量场![]() 在不同方向上的变化率一般来说是不同的,那么,可以设想,必定在某个方向上变化率为最大。为此,我们定义一个矢量
在不同方向上的变化率一般来说是不同的,那么,可以设想,必定在某个方向上变化率为最大。为此,我们定义一个矢量![]() ,其方向就是函数
,其方向就是函数![]() 在点
在点![]() 处变化率为最大的方向,其大小就是这个最大变化率的值,这个矢量
处变化率为最大的方向,其大小就是这个最大变化率的值,这个矢量![]() 称为函数
称为函数![]() 在点
在点![]() 处的梯度,记为:
处的梯度,记为:
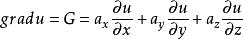
算子![]() 与标量函数
与标量函数![]() 相乘为一矢量函数。在直角坐标系中,梯度又可以表示为:
相乘为一矢量函数。在直角坐标系中,梯度又可以表示为:
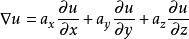
另外,以后还会经常用到标量拉普拉斯算子,即: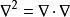 。在直角坐标系中标量函数的拉普拉斯表达式为:
。在直角坐标系中标量函数的拉普拉斯表达式为: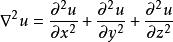 。
。
标量函数![]() 在圆柱坐标系中的梯度和拉普拉斯表达式分别为:
在圆柱坐标系中的梯度和拉普拉斯表达式分别为:
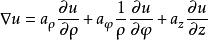
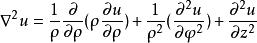
标量函数![]() 在球坐标系中的梯度和拉普拉斯表达式分别为:
在球坐标系中的梯度和拉普拉斯表达式分别为:
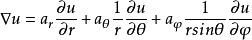
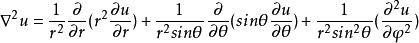
性质
(1)方向导数等于梯度在该方向上的投影,即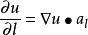 ;
;
(2)标量场![]() 中每一点
中每一点![]() 处的梯度,垂直于过该点的等值面,且指向函数
处的梯度,垂直于过该点的等值面,且指向函数![]() 增大的方向。也就是说,梯度就是该等值面的法向矢量。
增大的方向。也就是说,梯度就是该等值面的法向矢量。
(3)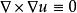 ,这个式子表明:如果有一个矢量场
,这个式子表明:如果有一个矢量场![]() 满足
满足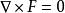 ,即
,即![]() 是一个无旋场,则矢量场
是一个无旋场,则矢量场![]() 可以用一个标量函数
可以用一个标量函数![]() 的梯度表示,即
的梯度表示,即![]() ,该标量函数称为势函数,对应的矢量场称为有势场。如静电场中的电场强度就可以用一个标量函数的梯度来表示。[3]
,该标量函数称为势函数,对应的矢量场称为有势场。如静电场中的电场强度就可以用一个标量函数的梯度来表示。[3]
标量场和矢量场
在一定的单位制下,用一个实数就足以表示的物理量是标量,如时间、质量、温度等;在这里,实数表示的是这些物理量的大小。[4]
和标量不同,矢量是除了要指明其大小还要指明其方向的物理量,如速度、力、电场强度等;矢量的严格定义是建立在坐标系的旋转变换基础上的。常见的矢量场包括Maxwell场、重矢量场。[4]



 求购
求购






