- 模糊测度论

模糊测度论
基本介绍
所谓积分,无论是黎曼积分还是勒贝格积分都不外乎是被积函数和测度函数的一种内积,不同的只是以不同的测度为基础。因此研究模糊积分要从研究模糊测度开始。
模糊测度有多种解释,M.Sugeno对模糊测度做了这样的解释:设有某个元素![]() ,我们猜想x可能属于A的某个元素A(即A∈A,且
,我们猜想x可能属于A的某个元素A(即A∈A,且![]() )。这种猜想是不确定的,是模糊的。
)。这种猜想是不确定的,是模糊的。
一个确定的点对于一个模糊集合的隶属程度,是经典集合论中点对集合属于关系的一种推广。模糊测度是普通属于关系的另一种推广,即一个尚未确定的点(信息不充分条件下)对于经典集合的属于关系。可能性测度在实际问题中是最常见的模糊测度,如海底矿藏测量。
为了研究模糊测度的结构和模糊积分的计算,日本著名学者M.Sugeno于1974年提出λ测度的概念,其核心思想是将概率测度的可加性放宽[1]。
基本概念
模糊测度
设(X,σ)是可测空间,如果映射 满足:
满足:
1.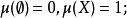
2.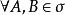 ,若
,若![]() ,有
,有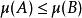 ;
;
3.若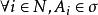 ,且
,且![]() 单调,有
单调,有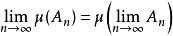 ;
;
则称μ为模糊测度,(X,μ)称为模糊测度空间。
模糊测度是由菅野道夫(M.Sugeno)于1974年提出的,它的研究是与具有主观性复杂系统的评价问题紧密相关的。目前,也有人将建立在模糊子集族构成的σ代数上的测度称为模糊测度。设Σ是X的模糊子集族,称Σ为由模糊子集构成的σ代数,如果Σ满足条件:
1.任何X的经典子集属于Σ。
2. ,此处
,此处
![]()
![]()
3.若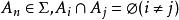 ,有
,有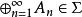 ,此处
,此处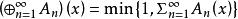
而从Σ到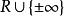 满足条件:
满足条件:
1.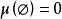 ;
;
2.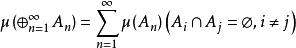
的映射称为模糊测度,这与第一种定义的模糊测度是根本不同的。
λ模糊测度
λ模糊测度(λ-fuzzy measure)是一种模糊测度,它是带参数λ的一种重要的模糊测度。设(X,σ)是可测空间,如果映射 满足以下条件:
满足以下条件:
1.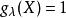 ;
;
2.对于σ中不相交的集合A与B,
![]()
3.对σ中的单调集合列![]() ,有
,有
![]() 则称gλ为λ模糊测度,这里一般假设参数λ>-1,当λ=0时,λ模糊测度为概率测度。若论域X是有限集,则当λ≥0时,λ模糊测度为信任测度;当-1<λ≤0时,λ模糊测度为似然测度。
则称gλ为λ模糊测度,这里一般假设参数λ>-1,当λ=0时,λ模糊测度为概率测度。若论域X是有限集,则当λ≥0时,λ模糊测度为信任测度;当-1<λ≤0时,λ模糊测度为似然测度。
设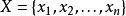 ,模糊分布函数H(x)满足
,模糊分布函数H(x)满足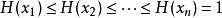 ,记
,记
![]()
![]()
对任何A⊂X,定义
![]() 则gλ是λ模糊测度。若H(xi)表示系统对xi的满意度,则H关于gλ的模糊积分表示系统整体的满意度[2]。
则gλ是λ模糊测度。若H(xi)表示系统对xi的满意度,则H关于gλ的模糊积分表示系统整体的满意度[2]。

-
传感器网络覆盖定位模糊信息处理方法
2025-08-10 19:21:00 查看详情 -
我国商业银行违约风险测度模型研究
2025-08-10 19:21:00 查看详情


 求购
求购










