- 负定矩阵

负定矩阵
意义
矩阵与方程组、行列式联系紧密,又是与自然科学和工程技术相关的数学应用的内容,矩阵变换是基本的数学方法,矩阵在数学中,乃至其他学科中应用广泛。负定矩阵是矩阵类中的一种特殊矩阵,它在矩阵理论中占有重要地位。负定矩阵可以看成是与正定矩阵对应的概念,负定矩阵与正定矩阵有着许多相似的性质。
定义
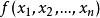 是一个二次型,对于任意一组不全为0的实数
是一个二次型,对于任意一组不全为0的实数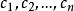 ,如果都有
,如果都有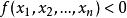 ,那么
,那么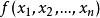 是负定的。
是负定的。
实对称矩阵A是负定的,如果二次型 负定[2]
负定[2]
性质
性质1:若矩阵![]() 是负定矩阵,则
是负定矩阵,则 是负定二次型。[2]
是负定二次型。[2]
性质2:若矩阵![]() 是负定矩阵,则实二次型
是负定矩阵,则实二次型 的负惯性指数等于
的负惯性指数等于![]()
性质3:若矩阵![]() 是负定矩阵,则有可逆矩阵
是负定矩阵,则有可逆矩阵![]() ,使
,使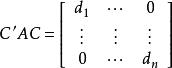 ,其中,
,其中,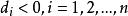
性质4:若矩阵![]() 是
是![]() 阶负定矩阵,当
阶负定矩阵,当![]() 是偶数时,
是偶数时,![]() ,当
,当![]() 是奇数时,
是奇数时,![]()
性质5:若矩阵![]() 是
是![]() 阶负定矩阵,则
阶负定矩阵,则![]() 的偶数阶顺序主子式大于 0,奇数阶顺序主子式小于 0
的偶数阶顺序主子式大于 0,奇数阶顺序主子式小于 0
性质6:若矩阵![]() 是负定矩阵,则
是负定矩阵,则![]() 合同于
合同于![]()
性质7:若矩阵![]() 是负定矩阵,则
是负定矩阵,则![]() 也是负定矩阵
也是负定矩阵
性质8:若矩阵![]() 是负定矩阵,则
是负定矩阵,则![]() 的所有特征值小于 0
的所有特征值小于 0
性质9:若矩阵![]() 是负定矩阵,则
是负定矩阵,则![]() 也是负定矩阵
也是负定矩阵
性质10:若矩阵![]() 是负定矩阵,则
是负定矩阵,则![]() 是正定矩阵
是正定矩阵
性质11:若矩阵![]() 是负定矩阵,则当
是负定矩阵,则当![]() 是偶数时,
是偶数时,![]() 是负定矩阵,当
是负定矩阵,当![]() 是奇数时,
是奇数时,![]() 是正定矩阵
是正定矩阵
性质12:若矩阵![]() 是负定矩阵,存在可逆实矩阵
是负定矩阵,存在可逆实矩阵![]() 使
使
判定定理
定理1:矩阵![]() 负定的充分必要条件是它的特征值都小于零
负定的充分必要条件是它的特征值都小于零
推论1:若矩阵![]() 是负定矩阵,则当
是负定矩阵,则当![]() 是偶数时,
是偶数时,![]() 是负定矩阵,当
是负定矩阵,当![]() 是奇数时,
是奇数时,![]() 是正定矩阵
是正定矩阵
推论2:设A是对称矩阵, 其中![]() 是矩阵A的特征值,当实数
是矩阵A的特征值,当实数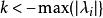 , 则
, 则![]() 是负定矩阵
是负定矩阵
推论3:任意对称矩阵![]() , 必有实数
, 必有实数![]() , 使得
, 使得![]() 都是负定矩阵
都是负定矩阵
定理2:若矩阵![]() 是负定矩阵的充要条件是负惯性指数等于
是负定矩阵的充要条件是负惯性指数等于![]()
推论4:若矩阵![]() 是
是![]() 阶负定矩阵,则
阶负定矩阵,则![]() 的偶数阶顺序主子式大于 0,奇数阶顺序主子式小于 0
的偶数阶顺序主子式大于 0,奇数阶顺序主子式小于 0
例题
例1. 判断下面的矩阵是否负定:
解:特征多项式为:
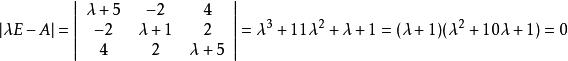
得到特征根: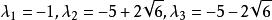 ,即特征值全部小于0,故该矩阵是负定矩阵。
,即特征值全部小于0,故该矩阵是负定矩阵。
例2. 判断二次型是否负定: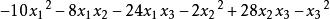
解:易知:二次型对应的矩阵为: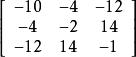
它的一阶顺序主子式
二阶顺序主子式: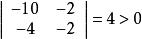
三阶顺序主子式: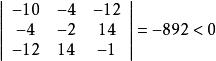
得到矩阵A是负定的, 所以上述二次型为负定二次型[3]



 求购
求购
