- 锥面

锥面
定义
通过一个定点V且与定曲线r(它不过定点V)相交的所有直线构成的曲面称为锥面;定点V叫做顶点。定曲线C叫做锥面的准线,构成曲面的每一条直线叫做母线。设锥面的准线![]() 的方程为
的方程为
![]() 那么通过顶点
那么通过顶点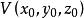 和准线
和准线![]() 上一点
上一点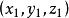 的直线即锥面的母线方程是[2]
的直线即锥面的母线方程是[2]
![]() 令上式的比值等
令上式的比值等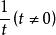 而得
而得
![]()
![]()
因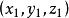 是准线
是准线![]() 上的点,故适合式
上的点,故适合式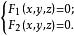 ,将上式代入,然后再消去t,即得锥面的普通方程。 特别地,如果锥面的顶点为坐标原点,准线为[2]
,将上式代入,然后再消去t,即得锥面的普通方程。 特别地,如果锥面的顶点为坐标原点,准线为[2]
![]() 那么锥面的方程就是
那么锥面的方程就是
![]() 事实上,因母线的方程为
事实上,因母线的方程为
![]() 又
又
![]()
消去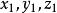 便得[2]
便得[2]
![]()
定理
以原点为顶点的锥面方程是关于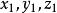 的齐次方程,反之,一个含
的齐次方程,反之,一个含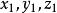 的齐次方程
的齐次方程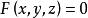 的图形总是顶点位于原点的锥面。[2]
的图形总是顶点位于原点的锥面。[2]
事实上.设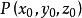 是曲面
是曲面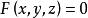 上的一点(但不是原点)。即
上的一点(但不是原点)。即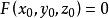 ,则直线OP上的任意一点M的坐标为
,则直线OP上的任意一点M的坐标为
![]() 一定也适合方程
一定也适合方程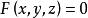 ,因为
,因为
![]()
这里的n是所给齐次方程的次数,这表示直线OP上任意一点都在曲面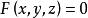 上,因此该曲面是由过原点的直线构成的,根据定义,这曲面是以原点为顶点的锥面。[2]
上,因此该曲面是由过原点的直线构成的,根据定义,这曲面是以原点为顶点的锥面。[2]
例题
求以原点为顶点,以椭圆
![]()
为准线的锥面(图1)的方程。[2]
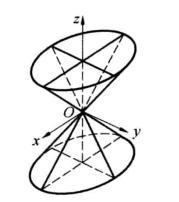 图1
图1
解据式
![]()
知,所求锥面的方程是
![]()
即
![]()
这是关于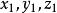 的二次齐次方程,这锥面叫做二次锥面,当a=b时,就是圆锥面。
的二次齐次方程,这锥面叫做二次锥面,当a=b时,就是圆锥面。



 求购
求购

