插补

       插补 （Interpolation）

　　在数控机床中，刀具不能严格地按照要求加工的曲线运动，只能用折线轨迹逼近所要加工的曲线。

　　插补（interpolation）定义：

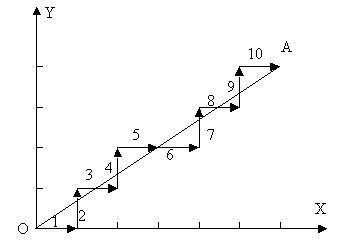　　机床数控系统依照一定方法确定刀具运动轨迹的过程。也可以说，已知曲线上的某些数据，按照某种算法计算已知点之间的中间点的方法，也称为“数据点的密化”。

　　数控装置根据输入的零件程序的信息，将程序段所描述的曲线的起点、终点之间的空间进行数据密化，从而形成要求的轮廓轨迹，这种“数据密化”机能就称为“插补”。

　　插补计算就是数控装置根据输入的基本数据，通过计算，把工件轮廓的形状描述出来，边计算边根据计算结果向各坐标发出进给脉冲，对应每个脉冲，机 床在响应的坐标方向上移动一个脉冲当量的距离，从而将工件加工出所需要轮廓的形状。

这个概念般是用在计算机图形显示,或则数控加工的近似走刀等情况下的.

以数控加工为例子

一个零件的轮廓往往是多种多样的,有直线,有圆弧,也有可能是任意曲线,样条线等. 数控机床的刀具往往是不能以曲线的实际轮廓去走刀的,而是近似地以若干条很小的直线去走刀,走刀的方向一般是x和y方向.

插补方式有:直线插补,圆弧插补,抛物线插补,样条线插补等

所谓直线插补就是只能用于实际轮廓是直线的插补方式(如果不是直线,也可以用逼近的方式把曲线用一段段线段去逼近,从而每一段线段就可以用直线插补了).首先假设在实际轮廓起始点处沿x方向走一小段(一个脉冲当量),发现终点在实际轮廓的下方,则下一条线段沿y方向走一小段,此时如果线段终点还在实际轮廓下方,则继续沿y方向走一小段,直到在实际轮廓上方以后,再向x方向走一小段,依次循环类推.直到到达轮廓终点为止.这样,实际轮廓就由一段段的折线拼接而成,虽然是折线,但是如果我们每一段走刀线段都非常小(在精度允许范围内),那么此段折线和实际轮廓还是可以近似地看成相同的曲线的--------这就是直线插补.

联动与插补

决定质点空间位置需要三个坐标，决定刚体空间位置需要六个坐标。

　　一个运动控制系统可以控制的坐标的个数称做该运动控制系统的轴数。

　　一个运动控制系统可以同时控制运动的坐标的个数称做该运动控制系统可联动的轴数。

　　联动各轴的运动轨迹具有一定的函数关系，例如直线，园弧，抛物线，正弦曲线。

　　直接计算得出运动轨迹的坐标值往往要用到乘除法，高次方，无理函数，超越函数，会占用很多的CPU时间。

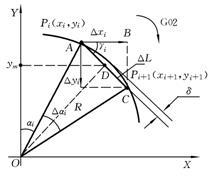
　　为了实时快速控制运动轨迹，往往预先对运动轨迹进行直线和圆弧拟合，拟合后的运动轨迹仅由直线段和圆弧段所组成，而计算运动轨迹时，每一点的运动轨迹跟据前一个坐标点的数据通过插补运算得到，这样就把计算简化为增量减量移位和加减法。

　　实现多轴联动的直线插补并不困难，圆弧插补一般为两轴联动。

　　实现插补运算可以有多种算法，例如 "DDA 算法"，"逐点比较法"，"正负法"，"最小偏差法（Bresenham 算法）"等，其中最小偏差法具有最小的偏差和较快的运行速度。